Question

A light rod of length L has two masses m₁ and m₂ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the Centre of mass is:-
(a). $\left( {{m_1} + {m_2}} \right){l^2}$\[\]
(b). $\sqrt {{m_1} + {m_2}} {l^2}$
(c). $\dfrac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}$
(d). $\dfrac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}{l^2}$

Answer 1

Hint: The moment of inertia is also known as mass moment of inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis similar to how mass determines the force needed for the desired acceleration. In order to solve this question I should have an idea about moments of inertia.

Complete step by step solution:
Moment of inertia (I) is defined as the ratio of the net angular momentum (L) of a system to its angular velocity (w) around a principal axis i.e. $l = \dfrac{L}{W}$. Its shape of the body does not change then its moment of inertia appears in Newton’s law of motion as the ratio of an applied torque(T) on a body is the angular acceleration $T = 1$$x$ or simple pendulum, this definition yields a formula for the moment of inertia I in terms of the mass m of the pendulum and its distance r from the pivot point as I=mr². In general given an object of mass ma, an effective radius K can be defined, dependent on a particular axis of isolation, with such a value that its moment of inertia around the axis is I=MK² Where K is known as the radius of gyration around the axis.

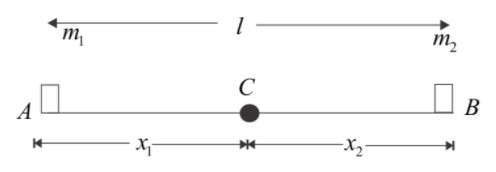
So center of mass from $m_1$ is =${x_1} = \dfrac{{{m_1}l + {m_2}(0)}}{{{m_1} + {m_2}}}$ = $\dfrac{{{m_1}l}}{{{m_1} + {m_2}}}$
Hence moment of inertia of masses about the center of mass = ${m_1}{x_1}^2 + {m_2}{x_2}^2$
= ${m_1}{\left( {\dfrac{{{m_2}l}}{{{m_1} + {m_2}}}} \right)^2} + {m_2}\left( {\dfrac{{{m_1}l}}{{{m_1} + {m_2}}}} \right)$
= \[\dfrac{{\left( {{m_1}{m_2}} \right)\left( {{m_1} + {m_2}} \right){l^2}}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\]
= \[\dfrac{{\left( {{m_1}{m_2}} \right){l^2}}}{{\left( {{m_1} + {m_2}} \right)}}\]

Hence option (c) is correct.

Note: The formula for moment of inertia is the sum of the product of mass of each particle with the square of its distance from the axis of the rotation. The formula of moment of Inertia is expressed as \[l = \sum\limits_{}^{} {m_ir_i{^2}} \]. The moment of Inertia depends on mass of the body, shape and size of the body, and distribution of mass about the axis of rotation. All these factors.