Question

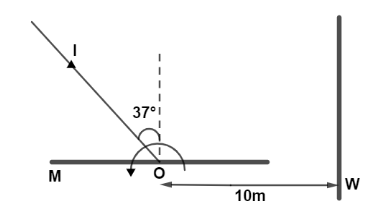
A light ray I is incident on a plane mirror M. The mirror is rotated in direction as shown in figure by an arrow at frequency $\dfrac{9}{\pi }rpm$ the light reflected by mirror is received on the wall at a distance of $10m$ from the axis of rotation. When the angle of incidence becomes $37^\circ $ the speed of the spot a point) on the wall is

A. $10\,m{\sec ^{ - 1}}$
B. $1000\,m{\sec ^{ - 1}}$
C. $500\,m{\sec ^{ - 1}}$
D. None of these

Answer 1

Hint: in order to solve this question we need to understand the rotation of reflected light if the plane mirror is rotated. So first a plane mirror is a regular reflection surface from one side and the other side of the mirror is silvered. Now when an incident light falls on a plane mirror at some angle with normal then it gets reflected at the same angle. However, if a plane mirror is rotated by some angle the normal also shifts by the same angle and hence the reflected ray rotates by twice the angle of rotation of the mirror.

Complete step by step answer:
We know that the reflected ray rotates by twice the angle of rotation of the mirror. Since the angular frequency is directly proportional to angle of rotation so if the plane mirror rotates by an angle $\theta $ or with angular velocity $\omega $ then the reflected ray rotates by an angle $2\theta $ or with angular velocity, $\omega ' = 2\omega $

Given frequency, $f = \dfrac{9}{\pi }{\sec ^{ - 1}}$
So $\omega = 2\pi f$
Putting values we get, $\omega = 2\pi \times \dfrac{9}{\pi }$
$\omega = 18rad{\sec ^{ - 1}}$
So reflected rotates by, $\omega ' = 2\omega $
Putting values we get, $\omega ' = 2 \times 18$
$\omega ' = 36\,rad\,{\sec ^{ - 1}}$

Since, $\omega ' = \left| {\dfrac{{d\theta }}{{dt}}} \right|$
$\left| {\dfrac{{d\theta }}{{dt}}} \right| = 36\,rad\,{\sec ^{ - 1}} \to (ii)$
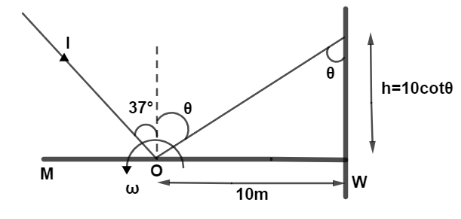
So from trigonometric ratio we can see from diagram, $h = 10\cot \theta $
Here, $h$ is the height of the spot on the wall.
Speed of spot is given by $v = \left| {\dfrac{{dh}}{{dt}}} \right| \to (i)$
Differentiating h with respect to t we get, $\left| {\dfrac{{dh}}{{dt}}} \right| = \left| {\dfrac{{d(10\cot \theta )}}{{dt}}} \right|$
$\left| {\dfrac{{dh}}{{dt}}} \right| = \left| { - 10\cos e{c^2}\theta \dfrac{{d(\theta )}}{{dt}}} \right|$

Since the incident light is at angle $\theta = 37^\circ $. Putting values we get,
$\left| {\dfrac{{dh}}{{dt}}} \right| = \left| { - 10\cos e{c^2}37\dfrac{{d(\theta )}}{{dt}}} \right|$
$\Rightarrow \left| {\dfrac{{dh}}{{dt}}} \right| = \left| { - \dfrac{{10}}{{0.36}}\dfrac{{d(\theta )}}{{dt}}} \right|$
Using (ii) we get,
$\left| {\dfrac{{dh}}{{dt}}} \right| = \left| { - \dfrac{{10}}{{0.36}} \times 36} \right|$
$\therefore \left| {\dfrac{{dh}}{{dt}}} \right| = 1000\,m{\sec ^{ - 1}}$
Using value of $\left| {\dfrac{{dh}}{{dt}}} \right|$ in equation (i) we get, $v = 1000\,m{\sec ^{ - 1}}$

So the correct option is B.

Note: It should be remembered that while the rotation of the reflected ray also rotates, the image size always remains constant and hence the image always forms on spot. Also plane mirrors emphasize regular reflection while in real life we often encounter diffuse reflection. As regular reflection is one in which incident angle is equal to reflected angle while in diffuse reflection it is not equal to reflected angle. Also the angle should always be measured from normal.