Question

A light beam of diameter $\sqrt{3}R$ is incident symmetrically on a glass hemisphere of radius R and of refractive index $n=\sqrt{3}$. The radius of the beam at the base of the hemisphere is:

A. $\dfrac{R}{\sqrt{3}}$
B. $\dfrac{R}{2\sqrt{3}}$
C. $\dfrac{\sqrt{3}R}{2}$
D. $\dfrac{R}{2}$

Answer 1

Hint: To solve the given question, we must know about the geometry of a hemisphere and trigonometry. We also must know Snell's law for the refraction at an interface of two different mediums.

Formula used:
${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$

Complete step by step answer:
The parallel beam of light is incident on the glass hemisphere. Let us use the Snell’s law for refraction at the interface of air and the glass. According to the Snell’s law, ${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$ …… (i),
where i and r are the angles of incidence and refraction at the interface. ${{\mu }_{i}}$ is the refractive of the medium from which the light ray meets the interface and ${{\mu }_{r}}$ is the refractive index of the medium into which the light ray enter after refraction.
Let us analyse the refraction of the outermost ray of light.
Let the normal at the interface as shown in the figure below (the normal a sphere passes through its centre).

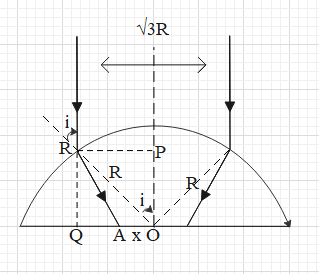
From the figure, we get that $\sin i=\dfrac{\dfrac{\sqrt{3}R}{2}}{R}=\dfrac{\sqrt{3}}{2}$.
 $\Rightarrow i={{\sin }^{-1}}\dfrac{\sqrt{3}}{2}={{60}^{\circ }}$
In this case, ${{\mu }_{i}}=1$ and ${{\mu }_{r}}=\sqrt{3}$.
Substitute the values of ${{\mu }_{i}}$ , ${{\mu }_{r}}$ and i in (i).
$\Rightarrow 1.\sin ({{60}^{\circ }})=\sqrt{3}\sin r$
$\Rightarrow \dfrac{\sqrt{3}}{2}=\sqrt{3}\sin r$
$\Rightarrow \sin r=\dfrac{1}{2}$
$\Rightarrow r={{\sin }^{-1}}\dfrac{1}{2}={{30}^{\circ }}$.
This means that the angle of refraction is ${{30}^{\circ }}$.
Let the radius of the light beam at the base be x.
Now, from the figure we get that $\cos i=\dfrac{OP}{R}$.
$\Rightarrow OP=R\cos i=R\cos {{60}^{\circ }}=\dfrac{R}{2}$.
And $OP=RQ$.
$\Rightarrow RQ=\dfrac{R}{2}$.
Now, consider $\Delta RQA$.
In this, $\cot {{30}^{\circ }}=\dfrac{\dfrac{R}{2}}{QA}$.
$\Rightarrow QA=\dfrac{R}{2\cot {{30}^{\circ }}}=\dfrac{R}{2\sqrt{3}}$.
But, $RP=QO$.
$\Rightarrow RP=QA+AO$
$\Rightarrow \sqrt{3}\dfrac{R}{2}=\dfrac{R}{2\sqrt{3}}+x$
$\Rightarrow x=\dfrac{\sqrt{3}R}{2}-\dfrac{R}{2\sqrt{3}}=\dfrac{3R-R}{2\sqrt{3}}=\dfrac{R}{\sqrt{3}}$
Therefore, the radius of the light beam at the base of the hemisphere is $\dfrac{R}{\sqrt{3}}$.

So, the correct answer is “Option A”.

Note:
Some students may use the formula for the refraction of light ray through a spherical interface of two
different mediums, i.e. $\dfrac{{{\mu }_{r}}}{v}-\dfrac{{{\mu }_{i}}}{u}=\dfrac{{{\mu }_{r}}-{{\mu }_{i}}}{R}$.
Here, ${{\mu }_{i}}$ and ${{\mu }_{r}}$ have the same meanings as discussed earlier. u is the position of the object and v is the position of the image. R is the radius of the spherical interface.
However, the equation is applicable only when the diameter of the beam is much smaller than the radius of the hemisphere.
Therefore, we cannot use the equation in the given case.