Question

A light beam emanating from the point (3, 10) reflects from the straight line 2x+y-6 = 0 then passes through the point (7, 2). Find the equations of the incident and reflected rays.

Answer 1

Hint: Let the points (3, 10) and (7, 2) be A and B respectively. We will find the slope of the line ax+by+c = 0 using $\dfrac{-a}{b}$and the slope of the line joining points $A\left( 3,10 \right)\text{ and }B\left( 7,2 \right)$using slope of line joining\[A\left( {{x}_{1}},{{y}_{1}} \right)\text{ and B}\left( {{x}_{2}},{{y}_{2}} \right)\text{ is }=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}.\] If we observe carefully, the line joining A and B is parallel to the given line 2x+y-6 = 0. Let the mid-point of the line segment is D and the point of reflection is C. By using the alternate angle property which states that the alternate angles formed by a transversal at the intersection of two parallel lines are equal, we can conclude that the two triangles$\Delta ACD\text{ , }\Delta BCD$ are congruent and we can conclude that the point of reflection ‘C’ will be the foot of perpendicular from the midpoint ‘D’ of the line segment AB to the given line.
Foot of perpendicular from the point is given by
 \[\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)\text{ to the line }ax+by+c=0\text{ is given by the formula} \\
 & \dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{-\left( a{{x}_{1}}+b{{y}_{2}}+c \right)}{{{a}^{2}}+{{b}^{2}}} \\
\end{align}\]
After getting the coordinates of C, we can use the points A, B and C to get the required line equations.

Complete step-by-step answer:
Given line L: 2x+y-6 = 0 and the points A (3, 10) and B (7, 2). Let the point of reflection be
C$({{x}_{1}},{{y}_{1}})$.
Slope of a line ax+by+c = 0 is $\dfrac{-a}{b}$
Using the formula, slope of the given line L=0 is $\dfrac{-2}{1}=-2$
Slope of line joining the points$A\left( {{x}_{1}},{{y}_{1}} \right)\text{ and B}\left( {{x}_{2}},{{y}_{2}} \right)\text{ is }=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}$.
Using the formula , slope of the line joining the points A and B is = $\dfrac{\left( 2-10 \right)}{\left( 7-3 \right)}=\dfrac{-8}{4}=-2$. As the slopes are equal, we can conclude that the lines L=0 and AB are parallel.

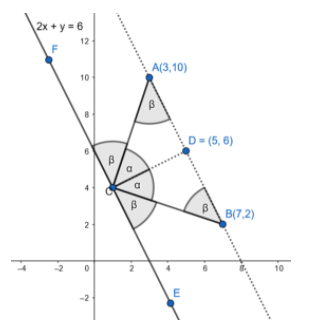
In the above figure, the lines AC and BC act as transversals for the parallel lines L=0 and AB.
From the property of alternate angles in parallel lines, we can conclude that
$\angle BAC=\angle ACF=\angle ABC=\angle BCE=\beta $
Let D be the point which is the point of intersection of the normal to the line L=0 at C and AB
From the property of reflection, $\angle ACD=\angle BCD$.
From the above properties and the common side CD we can conclude that$\Delta ACD\text{ and }\Delta BCD\text{ are congruent}$ and from this, we can conclude that D is the mid-point of AB.
Mid-point of $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\text{ is equal to }\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Using the formula, we get D=$\left( \dfrac{3+7}{2},\dfrac{10+2}{2} \right)=\left( 5,6 \right)$
We know that C is the foot of perpendicular from the point D to the line L=0.
Foot of perpendicular from the point is given by
 \[\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)\text{ to the line }ax+by+c=0\text{ is given by the formula} \\
 & \dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{-\left( a{{x}_{1}}+b{{y}_{2}}+c \right)}{{{a}^{2}}+{{b}^{2}}} \\
\end{align}\]
Applying the formula, we get the co-ordinates of C,
\[\begin{align}
  & \dfrac{x-5}{2}=\dfrac{y-6}{1}=\dfrac{-\left( 2\times 5+1\times 6-6 \right)}{{{2}^{2}}+{{1}^{2}}} \\
 & \dfrac{x-5}{2}=\dfrac{y-6}{1}=\dfrac{-\left( 10 \right)}{5} \\
 & \dfrac{x-5}{2}=\dfrac{y-6}{1}=-2 \\
 & x-5=-2\times 2\text{ ; }y-6=-2 \\
 & x=5-4=1\text{ ; }y=6-2=4 \\
 & \therefore \text{ C is (1,4)}\text{.} \\
\end{align}\]
The equation of the incident ray is given by the line AC and the equation of the reflected ray is given by the line BC.
Equation of a line passing through
\[\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\text{ is given by } \\
 & y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right) \\
\end{align}\]
Applying the above formula to get equation of line AC as
\[\begin{align}
  & y-10=\left( \dfrac{4-10}{1-3} \right)\left( x-3 \right) \\
 & y-10=\left( \dfrac{-6}{-2} \right)\left( x-3 \right) \\
 & y-10=\left( 3 \right)\left( x-3 \right) \\
 & y-10=3x-9 \\
 & 3x-y+1=0 \\
 & \\
\end{align}\]
Equation of line BC can be obtained as
\[\begin{align}
  & y-2=\left( \dfrac{4-2}{1-7} \right)\left( x-7 \right) \\
 & y-2=\left( \dfrac{2}{-6} \right)\left( x-7 \right) \\
\end{align}\]
\[\begin{align}
  & y-2=\left( \dfrac{-1}{3} \right)\left( x-7 \right) \\
 & 3y-6=-x+7 \\
 & x+3y-13=0 \\
\end{align}\]
$\therefore \text{ The incident and reflected rays are given by }3x-y+1=0\text{ and }x+3y-13=0\text{ respectively}\text{.}$

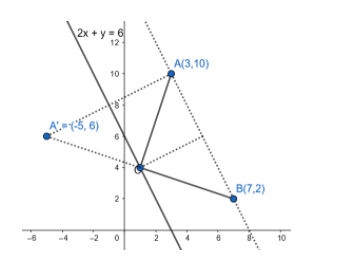
Note: An alternate way of doing this is by the property that the image of the point A with respect to the line L=0 will lie on the reflected line BC which gives us 2 points A’ and B to get the equation of reflected ray and with a similar approach we can get the incident ray.