Question

A length of wire carries a steady current, is bent first to form a plane circular coil of one turn, same length now bent more sharply to give three turns of smaller radius. Magnetic field becomes at centre:
A) 3 times
B) 1/3 times
C) 9 times
D) Unchanged

Answer 1

Hint: When a current carrying conductor is placed in space, a magnetic field is produced around it. In order to calculate the magnitude of the magnetic field, we have to use the Biot Savart’s law and apply it for the case of a circular coil with n turns. The mathematical form of Biot Savart’s law is given by:
Magnetic field at point at a distance of r, due to current carrying line element, $Idl$
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I \cdot dl}}{{{r^3}}}$
where ${\mu _0}$ = absolute permeability.

Complete answer:
Biot Savart’s law gives us an insight about the term magnetic field that arises due to presence of electric current.
Consider a line element in a conductor $dl$ through which current is flowing and an arbitrary point P at a distance of r from the conductor

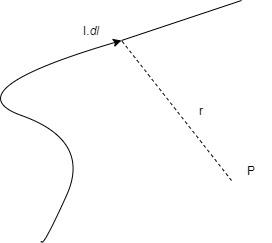
It states that, the magnetic field due to the line element $dl$is given by –
$dB \propto \dfrac{{I \cdot dl}}{{{r^3}}}$
By removing the proportionality symbol , we have –
$dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{I \cdot dl}}{{{r^3}}}$
where ${\mu _0}$ = absolute permeability.
By applying the Biot Savart’s law for a circular coil of n turns and integrating, we obtain the expression for the magnetic field at the centre of the coil as follows:
$\Rightarrow B = \dfrac{{{\mu _0}ni}}{{2r}}$
where ${\mu _0}$ = absolute permeability, $i$ = current flowing through the coil and r = radius of the coil.
Now, if the straight is bent into coil of one turn, the magnetic field at the centre of the coil of radius ${r_1}$ and number of turns, n = 1 is –
$\Rightarrow {B_1} = \dfrac{{{\mu _0}i}}{{2{r_1}}}$
Similarly, if the wire is bent three-times into radius ${r_2}$ ,
Number of turns, n = 3
The magnetic field at the centre due to the coil is given by –
$\Rightarrow {B_2} = \dfrac{{{\mu _0}3i}}{{2{r_2}}}$
Given that a single has been coiled into 3 turns from the same wire that is wound into a single turn, the radius becomes one-third of that of the coil of one turn. Hence,
$\Rightarrow {r_2} = \dfrac{{{r_1}}}{3}$
Substituting, we have –
$\Rightarrow {B_2} = \dfrac{{{\mu _0}3i}}{{2{r_1}}} \times 3$
By considering their ratio –
$\Rightarrow \dfrac{{{B_2}}}{{{B_1}}} = \dfrac{{\dfrac{{{\mu _0}3i}}{{2{r_1}}} \times 3}}{{\dfrac{{{\mu _0}i}}{{2{r_1}}}}} = 3 \times 3 = 9$
Thus, the magnetic field increases by 9 times.

Hence, the correct option is Option C.

Note: In competitive exams, for different numbers such as “same wire gives four, five or even six turns” , the students can use this shortcut. The magnetic field increases by the square of the number of turns mentioned in the question. For example, if the straight is turned n times, the magnetic field increases by ${n^2}$ times.