Question

A launching pad with a spaceship is moving along a circular orbit of the moon, whose radius $R$ is triple of that of moon ${{R}_{m}}$.the ship leaves the launching pad with a relative velocity equal to launching pad’s initial orbital velocity $\overset{\to }{\mathop {{v}_{o}}}\,$and the launching pad then falls on the moon. The angle $\theta $ with the horizontal at which the launching pad crashes into the surface if its mass is twice of the spaceship $m$.

Answer 1

Hint: Concept of conservation of linear and angular momentum to be applied here
In an isolated system when no external torque or force acts both linear and angular momentum remains constant. Also orbital velocity=$\sqrt{\dfrac{GM}{R}}$ where $G$is gravitational constant$R$is distance from the planet around which the launch pad is orbiting and $M$is mass of the moon.
Conservation of energy is also to be applied between the point when the launch pad is leaving to the point when it crashes on the moon.

 Complete step by step answer:

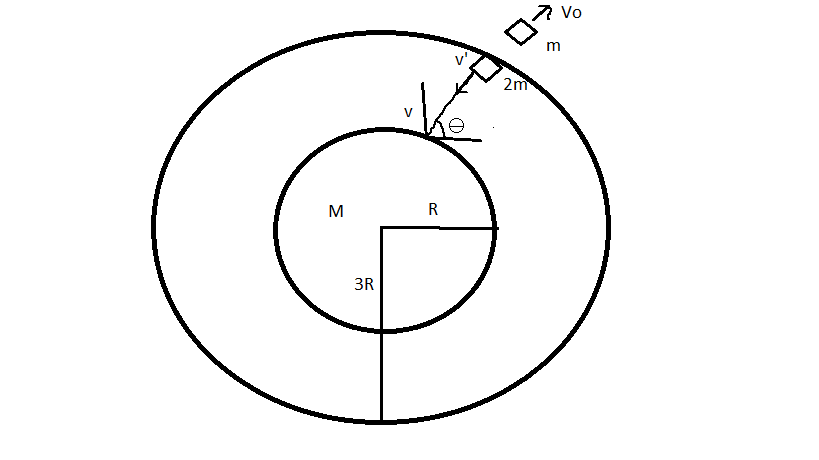
In the question it is given $R=3{{R}_{m}}$
Let us assume that the launch pad leaves the ship with a velocity of $V'$ and at the time of crashing makes an angle $\theta $ with the horizontal and lands with a velocity $V$.
The spaceship moves with orbital velocity ${{V}_{o}}$ relative to the launch pad which moves with $V'$ in the opposite direction .
So from the ground frame the actual velocity of the spaceship is ${{V}_{o}}+{{V}^{'}}$.
Mass of launch pad=$2m$ where $m$ is mass of spaceship
For finding $V'$ apply conservation of momentum before the launch pad leaves spaceship and after it
Initial momentum=final momentum
$\Rightarrow 3m\times {{V}_{o}}=2m\times {{V}^{'}}+\left( {{V}_{o}}+{{V}^{'}} \right)\times m$
$2m{{V}_{o}}=3mV'$
${{V}^{'}}=\dfrac{2}{3}{{V}_{o}}.......(1)$
Now applying conservation of energy between points when launch pad leaves spaceship and when it crashes on earth

${{\left( potential\,energy \right)}_{i}}+{{\left( kinetic\,energy \right)}_{i}}=\,{{\left( potential\,energy \right)}_{f}}+{{\left( kinetic\,energy \right)}_{f}}$
$\dfrac{-GM2m}{3R}+\dfrac{1}{2}2m{{\left( {{V}^{'}} \right)}^{2}}=\dfrac{-GM2m}{R}+\dfrac{1}{2}2m{{\left( V \right)}^{2}}$

$\dfrac{{{V}^{2}}}{2}=\dfrac{2GM}{3R}+\dfrac{{{\left( {{V}^{'}} \right)}^{2}}}{2}........\left( 2 \right)$

We know that $\,{{V}_{o}}^{2}=\dfrac{GM}{3R}$ using this result and $\left( 1 \right)$
Putting in $\left( 2 \right)$

$\dfrac{{{V}^{2}}}{2}=2{{V}_{o}}^{2}+\dfrac{2{{V}_{o}}{{^{2}}^{{}}}}{9}$

We get$V=\dfrac{2\sqrt{10}}{3}{{V}_{o}}......\left( 3 \right)$

From conservation of angular momentum of launch pad
We take horizontal component of velocity $V$which is $V\cos \theta $when equating angular momentum of launch pad when it crashes and when it just left the spaceship
Initial angular momentum=final angular momentum

$2m{{V}^{'}}\times 3R=2mV\cos \theta \times R$

$\cos \theta =\dfrac{3{{V}^{'}}}{V}$
Replacing values (1) from (3) and

$\cos \theta =\dfrac{3\times \dfrac{2}{3}{{V}_{o}}}{\dfrac{2\sqrt{10}}{3}{{V}_{o}}}$

$\cos \theta =\dfrac{3}{\sqrt{10}}$

The value of angle which the launch pad makes while crashing with horizontal has been found out.


Note:
Angular momentum can be expressed for both linear and rotational motion as well as for both combined too. $L=I\times \overset{{}}{\mathop w}\,$ where $I$ is moment of inertia and $w$ is angular velocity of rotational motion.
Gravitational potential energy Is the energy associated with a particle due to the gravitational field. When the object is released this energy gets converted into kinetic energy of the object.