Question

A large glass slab ($\mu =\dfrac{5}{3}$) of thickness 8cm is placed over a point source of light on a plane surface. It is seen that the light emerges out of the top surface of the slab from a circular area of radius R cm. What would be the value of R?

Answer 1

Hint: In the question it is given that the point source of light is kept under the slab. As the light enters the slab, it will undergo refraction and bend with respect to the incident surface. Further the light will escape from the other surface of the slab and in the question it is given that the light emerges out of the top surface of the slab from a circular area of radius R cm. To determine the radius of the circle, consider the rays that just refract along the circumference of the circle and using Snell’s law the radius can be determined accordingly.

Formula used:
$\dfrac{\sin i}{\sin r}=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}}$

Complete step-by-step answer:

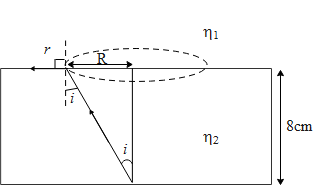
From the above figure we can see that the point source light when escapes the top surface of the slab forms circular region of radius R. If we consider any rays between the circular region they escape the surface and hence we see the circular region. The rays outside the circumference of the circle do not come out of the slab as they get reflected back into the slab. If we consider the rays on the circumference of the circle these rays should get reflected back such that the angle of refraction if just
${{90}^{\circ }}$ . let us say the refractive index of the slab be ${{\eta }_{2}}$ and that of air be ${{\eta }_{1}}$ . therefore from Snell’s law the relation between the angle of incidence ‘i’ and angle of refraction ‘r’ from the above figure is given by,
$\dfrac{\sin i}{\sin r}=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}}$
The sine of an angle is the ratio of the opposite side to that of the hypotenuse. Therefore from the figure the sine of angle of incidence is given by,
$\sin i=\dfrac{R}{\sqrt{{{R}^{2}}+{{8}^{2}}}}$
The angle of refraction for the outermost ray along the circumference makes an angle ${{90}^{\circ }}$. Hence from Snell’s law we get ‘R’ as,
$\begin{align}
  & \dfrac{\sin i}{\sin r}=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}} \\
 & \Rightarrow \dfrac{\dfrac{R}{\sqrt{{{R}^{2}}+{{8}^{2}}}}}{1}=\dfrac{1}{\dfrac{5}{3}},\because \sin {{90}^{\circ }}=1 \\
 & \Rightarrow {{\left( \dfrac{R}{\sqrt{{{R}^{2}}+{{8}^{2}}}} \right)}^{2}}={{\left( \dfrac{3}{5} \right)}^{2}} \\
 & \Rightarrow \dfrac{{{R}^{2}}}{{{R}^{2}}+64}=\dfrac{9}{25} \\
 & \Rightarrow (25-9){{R}^{2}}=576 \\
 & \Rightarrow 16{{R}^{2}}=576 \\
 & \Rightarrow {{R}^{2}}=36 \\
 & \therefore R=6cm \\
\end{align}$
Therefore the radius of the circle through which light emerges out of the top surface of the slab is 6cm.

Note: The refractive index of air is taken to be 1. This is due to the fact that light in vacuum and air has the same speed. From the centre of the circle the angle of incidence keeps on increasing and at a particular angle of incidence the light suffers total internal reflection and therefore we observe a distinguished circular boundary.