Question

A ladder is resting with one end in contact with the top of a wall of height 12 meters and the other end on the ground is at a distance of 5 meters from the wall.
The length of the ladder is (in m).......

Answer 1

Hint:
Here we will first draw the diagram based on the given information, which will be in the form of a right-angled triangle. We will then apply the Pythagoras theorem to find the length of the ladder. Here ladder will be the hypotenuse of this right-angled triangle.

Complete step by step solution:
 Here we need to find the length of the ladder which is resting on a wall.
We will first draw the figure and we will assume the point of contact of the ladder with the wall to be point \[A\] and we will assume the point of contact of the ladder with the floor to be point \[C\].
It is given that the height of the wall is 12 meters and the distance of the vase of the ladder from the wall is equal to 5 meters.

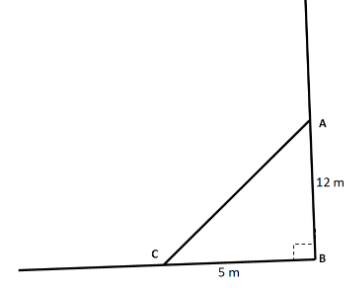
We can see that $\vartriangle ABC$ is a right angled triangle
Now, we will apply the Pythagoras theorem here.
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
Now, we will substitute the value of height and base here.
\[ \Rightarrow A{C^2} = {12^2} + {5^2}\]
On finding the squares, we get
\[ \Rightarrow A{C^2} = 144 + 25\]
On adding the numbers, we get
\[ \Rightarrow A{C^2} = 169\]
Now, we will take square root on both sides.
\[\begin{array}{l} \Rightarrow \sqrt {A{C^2}} = \sqrt {169} \\ \Rightarrow AC = 13\end{array}\]

Therefore, the length of the ladder is equal to 13 meters.

Note:
Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the square of the other two sides of the triangle. The hypotenuse is the longest side of the triangle. Pythagora's theorem can only be applied on a right angled triangle. As the diagram took the shape of a right angled triangle so we applied this theorem to find the length of the ladder.