Question

A kite flying a height ′ $h$ ′ mts has ′′ $x$ ′′ metres of string paid out at a time $t$ seconds. If the kite moves horizontally with constant velocity $v\,mts{\sec ^{ - 1}}$ . then the rate at which the string is paid out is
A. $$2$$
B. $\sqrt {{x^2} - {h^2}} mt{\sec ^{ - 1}}$
C. $$\dfrac{{\sqrt {{x^2} - {h^2}} }}{x}\,mt{\sec ^{ - 1}}$$
D. $$\dfrac{{\sqrt {{x^2} - {h^2}} }}{h}\,mt{\sec ^{ - 1}}$$

Answer 1

Hint: Firstly, note that the height will be vertical and the velocity of kite is given in horizontal direction. Also, the string will be inclined. All these three quantities will form a right-angled triangle. The velocity will be the rate of change in horizontal direction and the inclined length of strings rate of change is asked. So, obtain a relation between all three quantities and differentiate.

Complete step by step answer:
As discussed in the hint, let us draw the right-angled triangle.

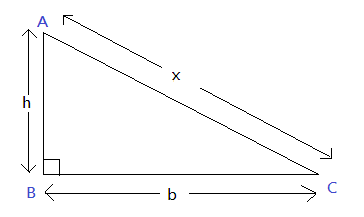
Here h is the height at which the kite is flying
x denotes the string and b is taken in horizontal direction.
As we can see that the triangle is a right-angled triangle, hence we can apply Pythagoras theorem as follows:
$$A{C^2} = A{B^2} + C{B^2}$$
$$ \Rightarrow {x^2} = {h^2} + {b^2}$$
$$ \Rightarrow x = \sqrt {{h^2} + {b^2}} $$ --equation $$1$$
Now, we have to find the rate of change of the length of string and we are given the rate of change in horizontal direction. The kite moves horizontally with a velocity $v\,mts{\sec ^{ - 1}}$ which means that:
$$\dfrac{{db}}{{dt}} = v$$ --equation $$2$$
as rate of change means change in quantity per unit time.
We have to find the value of $$\dfrac{{dx}}{{dt}}$$ --equation $$3$$
Note that the height at which the kite is flying is constant, so let’s differentiate equation $$1$$ with respect to time, we have
$$x = \sqrt {{h^2} + {b^2}} $$
Differentiating both sides with $$dt$$ we have
$$\dfrac{{dx}}{{dt}} = \dfrac{1}{{2\sqrt {{h^2} + {b^2}} }} \times 2b\dfrac{{db}}{{dt}}$$
Substituting value of $$\dfrac{{db}}{{dt}}$$ from equation $$2$$ , we have
$$\dfrac{{dx}}{{dt}} = \dfrac{{\sqrt {{x^2} - {h^2}} }}{x} \times v$$
Therefore, the rate at which the string is paid out is $$\dfrac{{\sqrt {{x^2} - {h^2}} }}{x}\,mt{\sec ^{ - 1}}$$

So, the correct answer is “Option B”.

Note:
Be careful while differentiating the equation. In the final step, we substituted the values from the first equation to convert the answer in the form of options. Please note that throughout the motion, the height does not change.
The velocity will be the rate of change in horizontal direction and the inclined length of strings rate of change.