Question

A) If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find \[AC\]
B) If AB = 5.6cm, AC = 4cm and DC = 3cm, find \[BC\]

Answer 1

Hint: This problem comes under properties of triangles. In a \[\vartriangle ABC\] and \[AD\] bisect $\angle A$, meeting side \[BC\] at \[D\]. Since \[\vartriangle ABC\] bisects then the triangle divides into two. With similarity of the triangle under if two triangles are similar then the sides are proportional using this property we solve and then basic mathematical calculation and complete step by step explanation.

Complete step-by-step answer:
A) If \[AB = 5.6cm\], \[BD = 3.2cm\] and \[BC = 6cm\], find \[AC\]

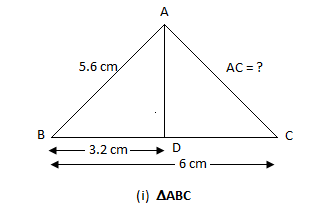
The \[AD\] is the bisector of $\angle A$,
We know that the \[BC = 6cm\], \[BD = 3.2cm\], we can find \[DC\], then
\[ \Rightarrow BC = BD + DC\]
Substituting the values of \[BC\] and \[BD\],
\[ \Rightarrow \;6 = 3.2 + DC\]
Solving for \[DC\],
\[ \Rightarrow DC = 6 - 3.2\]
Subtracting the terms we get,
\[DC = 2.8cm\]
In \[\vartriangle ABC\]
\[\angle BAD = \angle CAD\]
Since the Angles of triangle are equal then the triangles are proportional
\[ \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}}\]
Substituting the values of \[AB\], \[BD\] and \[CD\],
$ \Rightarrow \dfrac{{5.6}}{{AC}} = \dfrac{{3.2}}{{2.8}}$
 By rearranging we get,
$ \Rightarrow AC = \dfrac{{2.8 \times 5.6}}{{3.2}}$
We have to find the value of $AC$,
Hence, we are solving it for $AC$,
$AC = 4.9cm$
$\therefore $ Thus the value of $AC$ is \[4.9cm\]
B) If \[AB = 5.6cm\], \[AC = 4cm\] and \[DC = 3cm\], find \[BC\]

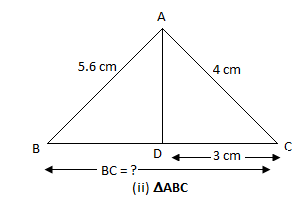
The \[AD\] is the bisector of $\angle A$,
We know that the \[AB = 5.6cm\], \[AC = 4cm\], and \[DC = 3cm\], we can find \[BD\], then
In \[\vartriangle ABC\]
\[\angle BAD = \angle CAD\]
Since the Angles of triangle are equal then the triangles are proportional
\[ \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{CD}}\]
$ \Rightarrow \dfrac{{5.6}}{4} = \dfrac{{BD}}{3}$
By rearranging, we get
$ \Rightarrow BD = \dfrac{{5.6 \times 3}}{4}$
We have to find the value of \[BD\],
Hence, we are solving it for \[BD\],
$ \Rightarrow BD = \dfrac{{16.8}}{4}$
Dividing the terms we get,
$BD = 4.2cm$
We need to find \[BC\],
$ \Rightarrow BC = BD + DC$
Substituting the value of \[BD\] and $DC$ to find the value of \[BC\],
$ \Rightarrow BC = 4.2 + 3$
Adding the terms we get,
$BC = 7.2cm$
$\therefore $ Thus the value of \[BC\] is \[7.2cm\]

Note: This kind of problem needs to know about the triangle clearly, the similarity of the triangle makes a huge part in it. The basic concepts of the triangle are similarly proportional with the bisector of the angle. The basic decimal multiplication and division has to take place on it. So, we need to know about the properties of a triangle clear with angle and sides.