Question

A horse is placed for grazing inside a rectangular field 40 m by 36 m and is tethered to one corner by a rope 14 m long. Over how much area can it graze?

Answer 1

Hint:
 Area is defined as the space inside a shape of any plane. If l is the length of the rectangle and b is the breadth of the rectangle then,
Area of rectangle is given by \[l \times b\]
Sector means the area enclosed by the portion of two radii and an arc.

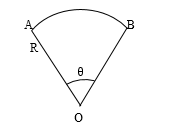
Area of sector is given by the formula,
\[ \Rightarrow \]\[\dfrac{\theta }{{{{360}^o}}} \times \pi {R^2}\]
Where θ is in degree and is the angle made by the arc AB at the centre and R is the radius of the circle of which the sector is a part.

Complete step by step solution:
Given Length of the Rectangular field = 40 m
Breadth of the Rectangular field = 36 m
Also the length of the rope through which the horse is tethered in one corner = 14 m

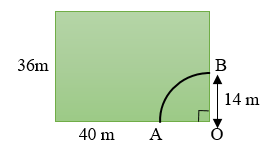
Now OA is the length of the rope and also the radius of the sector AOB, which is equal to 14 m
Also the angle AOB = 90°.
Then are that the horse can graze inside the rectangular field will be equal to the area of the sector AOB,
that is the area horse can graze.
=\[\dfrac{{angle{\text{ }}made{\text{ }}by{\text{ }}the{\text{ }}arc{\text{ }}AOB}}{{{{360}^o}}} \times \pi {R^2} = \dfrac{{90}}{{360}} \times \dfrac{{22}}{7} \times 14 \times 14\]
 \[ = \dfrac{1}{4} \times 22 \times 2 \times 14 = 154{m^2}\]
Where, (\[\pi \]=\[\dfrac{{22}}{7}\])
Hence the area over which horse can graze is 154 $m^2$.

Note:
Never forget to write the correct unit in your answer.
Unit of area will always be in the Square unit and the unit of all the data provided should be in the same unit. So the unit of length, breadth and the radius of the sector should be converted to the same unit.