Question

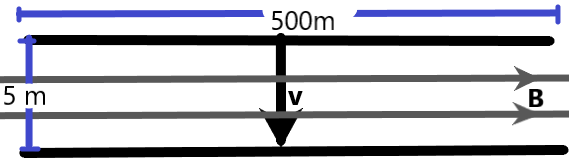
A horizontal telegraph wire 0.5km long running east and west 5m above the ground in a part of a circuit whose resistance is 2.5 \[\Omega \]. The wire falls to \[g=10m{{s}^{-2}}\text{ and }B=2\times {{10}^{-5}}Wb{{m}^{-2}}\], then the current induced in the circuit is –
A) 0.7 A
B) 0.04 A
C) 0.02 A
D) 0.01 A

Answer 1

Hint: We need to understand the relation between the free fall of a conducting wire of certain length and resistance into a magnetic field which is perpendicular to the wire in order to find the current induced in the wire due to this motion.

Complete Step-by-Step Solution:
We are given a 500 m long wire which was initially held horizontal to the base. A magnetic field travelling in the direction from east to west is present below the wire which is kept in the same direction. At some moment of time, the wire is left to fall freely under gravity through this magnetic field.

We can understand from the situation that the direction of velocity of the wire is perpendicular to the direction of the magnetic field. So, there is a possibility of induction of electromotive force in the wire.

The motional emf of a conducting wire moving perpendicular to the magnetic field is given as –
\[\begin{align}
  & \varepsilon =-\dfrac{d{{\phi }_{B}}}{dt} \\
 & \Rightarrow \varepsilon =Blv \\
 & \text{but,} \\
 & v=at \\
 & \therefore \varepsilon =Bl(at) \\
\end{align}\]
Where, a is the acceleration of the wire through the magnetic field, t is the time taken, B is the magnetic field strength and l is the length of the wire.

Using the equation of motion, we can find the time taken for the wire to reach the ground as –
\[\begin{align}
  & t=\sqrt{\dfrac{2h}{g}} \\
 & \Rightarrow t=\sqrt{\dfrac{2\times 5m}{10m{{s}^{-2}}}} \\
 & \therefore t=1s \\
\end{align}\]

We can find the current induced from the emf as –
\[\begin{align}
  & i=\dfrac{\varepsilon }{R} \\
 & \Rightarrow i=\dfrac{Bl(at)}{R} \\
 & \Rightarrow i=\dfrac{2\times {{10}^{-5}}Wb{{m}^{-2}}\times 500m\times 10m{{s}^{-2}}\times 1s}{2.5\Omega } \\
 & \therefore i=0.04A \\
\end{align}\]
The current induced in the circuit is 0.04 A.

Hence, the correct answer is option B.

Note:
The current induced in a conducting wire while travelling through a magnetic field can be zero if the motion of the wire does not have a perpendicular component of velocity. For a square loop, the sides parallel to the magnetic field don't have induced emf.