Question

A hollow metallic sphere of radius 10cm is given a charge of $3.2 \times {10^{ - 9}}C$. The electric field intensity at a point $4cm$ from the centre is
A) $9 \times {10^{ - 9}}N/C$
B) $288N/C$
C) $2.88N/C$
D) zero

Answer 1

Hint: The electric field intensity inside a hollow sphere is zero. We can use Gauss’ law of electricity to prove that the electric field intensity inside any hollow conductor is zero.

Complete step by step solution:

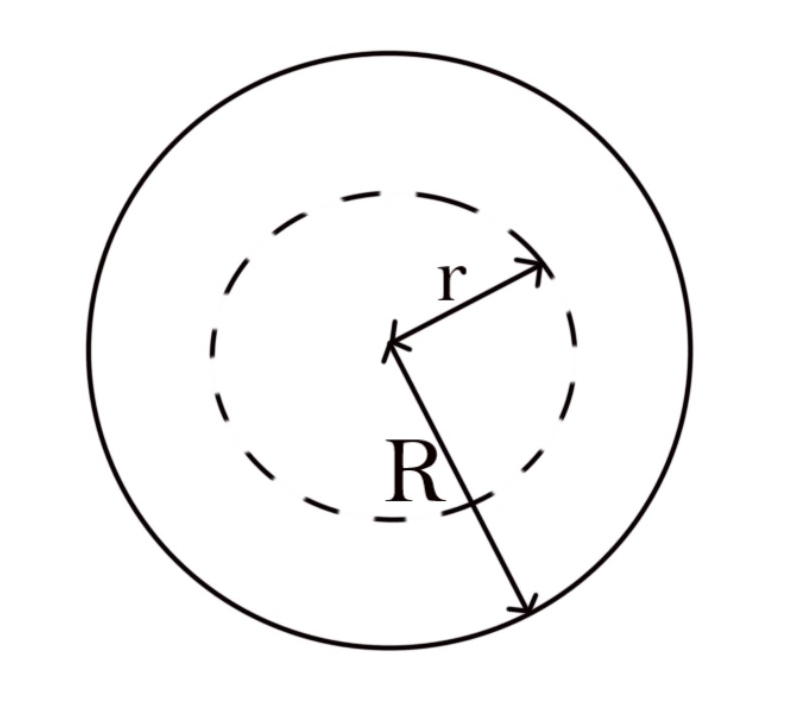
Let a spherical gaussian surface of radius $r$ having a concentric center with the charged sphere. The gaussian surface must be inside the charged surface because we want to calculate the electric field intensity inside the sphere.
The gaussian surface is shown in the figure.
According to the Gauss’ law of electricity,
$\oint {E.ds = \dfrac{{{q_{in}}}}{{{\varepsilon _0}}}} $
Where,
$E$ is the electric field intensity at a distance $r$ from the centre of the surface of radius $R$
$ds$ is the small area taken on the gaussian surface
${q_{in}}$ is the charge inside the gaussian surface.
It is given in the question that the sphere is metallic which means that all the charge will evenly distribute on the surface of the charged sphere and there is no charge inside the hollow sphere. So, ${Q_{in}}$ is zero.
Putting the values in Gauss’ law,
$\oint {E.ds = \dfrac{0}{{{\varepsilon _0}}}} $
Since the electric field is constant, the small area is integrated into the surface area of the gaussian surface,
$E(4\pi {r^2}) = \dfrac{0}{{{\varepsilon _0}{R^3}}}$
$E = 0$

$\therefore $ Electric field inside the conductor is zero. So, option (D) is correct.

Note:
Electric field intensity inside any conductor is always zero. This is because when the electric field passes through a conductor the negative charges start moving in the direction opposite to that of the applied electric field, while the positive charges are pushed by the electric field. Thus, on one side you will find only negative charges and the positive charges on another site. Now the electric field inside the conductor will start flowing due to induced charges from positive to negative against the applied electric field. Hence, the fields get cancelled inside the conductor. Leaving zero electric fields inside the conductor.