Question

A hollow dielectric sphere has $R_{1}$ and $R_{2}$ as its inner and outer radii. The total charge carried by the sphere is $+Q$ which is uniformly distributed throughout the dielectric sphere between $R_{1}$ and $R_{2}$ . The electric field $R_{1} < r < R_{2}$ is given by:
\[\begin{align}
  & A.\dfrac{Q}{4\pi r{{\varepsilon }_{0}}{{R}_{1}}} \\
 & B.\dfrac{Q}{4\pi r{{\varepsilon }_{0}}r} \\
 & C.\dfrac{Q}{4\pi r{{\varepsilon }_{0}}R_{1}^{2}} \\
 & D.\dfrac{Q({{r}^{3}}-R_{1}^{2})}{4\pi r{{\varepsilon }_{0}}{{r}^{2}}(R_{2}^{3}-R_{1}^{3})} \\
\end{align}\]

Answer 1

Hint: Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. Then to find the electric field inside the shell we can use the formula of electric field. Since here, we have a spherical sphere, we can use the volume density of to calculate the charge on the sphere.

Formula used:
$E=\dfrac{F}{q}$

Complete step by step answer:
Consider a spherical sphere that has $R_{1}$ and $R_{2}$ as its inner and outer radii, given that the charge $Q$ be uniformly distributed throughout the sphere. Let $r$ be such that $R_{1} < r < R_{2}$ as shown in the figure. Also let this region contain some $q$ charge.

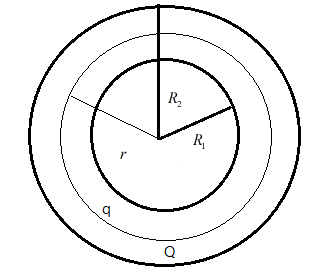
Let us assume that $\rho$ is the volume density of the hollow sphere, it is the ratio between the charge and the volume of the sphere, then we can say that $\rho=\dfrac{Q}{\dfrac{4\pi}{3}(R_{2}^{3}-R_{1}^{3})}$
We can then say that the charge $q=\rho\times\dfrac{4}{3}\pi(r^{3}-R_{1}^{3})=\dfrac{Q}{\dfrac{4\pi}{3}(R_{2}^{3}-R_{1}^{3})}\times\dfrac{4}{3}\pi(r^{3}-R_{1}^{3})=
\dfrac{Q(r^{3}-R_{1}^{3})}{(R_{2}^{3}-R_{1}^{3})}$
$\implies q=\dfrac{Q(r^{3}-R_{1}^{3})}{(R_{2}^{3}-R_{1}^{3})}$
We know that electric field $E$ is the electric force per unit charge, then $E=\dfrac{kq}{r^{2}}$ where, $r$ is the distance between the charge and $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is a constant and $r$ is the distance between the unit charges.
Substituting for $q$, we get $E=\dfrac{1}{4\pi\epsilon_{0}r^{2}} \times\left(\dfrac{Q(r^{3}-R_{1}^{3})}{(R_{2}^{3}-R_{1}^{3})}\right)$
Hence the answer is option \[D.\dfrac{Q({{r}^{3}}-R_{1}^{2})}{4\pi r{{\varepsilon }_{0}}{{r}^{2}}(R_{2}^{3}-R_{1}^{3})}\]
Additional information:
Electric field is in the direction of the force. Usually, the electric field of a point positive charge is radially outwards, whereas the electric field of a point negative charge is radially inwards to the charge. However, the electric field also depends on the symmetry of the charge carrying conductor

So, the correct answer is “Option A”.

Note:
We can also use gauss law to solve the problem as we need to calculate the electric field due to a charge. From Gauss law, we know that the total electric flux through a closed surface is equal to $\dfrac{1}{\epsilon_{0}}$ times the charge enclosed in the surface, and it is given by $\Phi_{E}=\dfrac{q}{\epsilon_{0}}$.