Question

A high-resistance voltmeter connected across the terminals of a battery reads $15\;V$. When an ammeter is included in the circuit, the voltmeter reads $9.0\;V$ and the ammeter reads $1.5\;A$. Find internal resistance of the battery.

Answer 1

Hint: We know that the ammeter and voltmeter are small meters which are connected to a circuit, to measure the current and the voltage of the circuit respectively. An ammeter is connected in series with a circuit, whereas the voltmeter is connected in parallel with the circuit.

 Formula used:
$V=IR$
$E=V+Ir$

Complete step by step answer:
Consider the circuit as shown below, where $E$ is the emf of the cell , $I$ is the current in the circuit and $r\;,R$ is the internal resistance of the battery and the external resistance of the circuit. Let $A$ and $V$ be the ammeter and the voltmeter connected to the circuit.

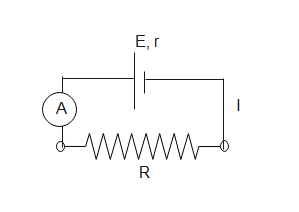
Since $V$ shows $15\;V$ across the battery, we can say that $V=E=15V$.
When the battery is connected to the circuit, then we have $I=1.5A$ when $V=9V$. Since the ammeter is connected in series with the circuit, we can say that the same current flows through the internal resistance $r$.
Then from the circuit, we have $E=V+Ir$, substituting the vales , we have
$\implies 15=9+1.5r$
$\implies r=\dfrac{6}{1.5}=4\Omega$
Thus the internal resistance of the battery is $4\Omega$

Note: Since the ammeter has very low resistance, when connected to the circuit in series, it draws some current . When connected to the circuit. However this current is comparable, when compared to the current in the circuit and thus can be taken to be the same. Similarly, a voltmeter has a high resistance and is connected in parallel to avoid the flow of current through it. Also note the internal resistance of the battery is smaller and negligible as compared to the external resistance in the circuit.