Question

A hemispherical depression is cut out from one face of the cubical wooden block such that the diameter $l$ of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer 1

Hint- Area of top of the hemispherical part\[ = \pi {r^2}\] sq. Unit, Curved surface area of the hemispherical part\[ = 2\pi {r^2}\] sq. unit

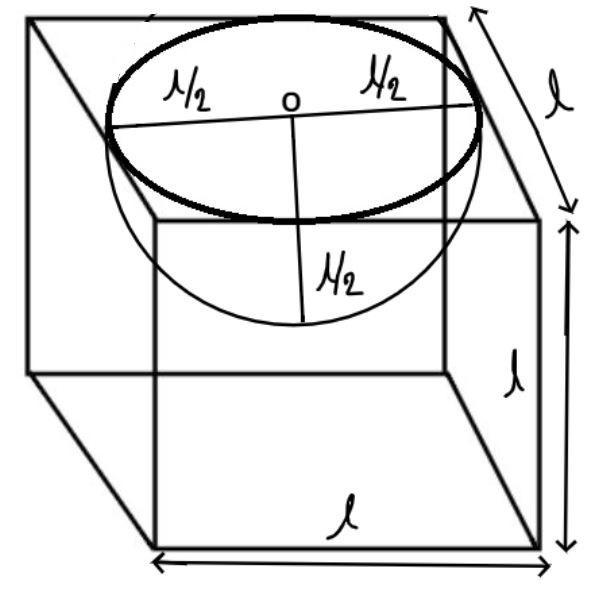
Consider the diagram shown above.
It is given that a hemisphere of diameter $l$unit is cut out from the top face of the cubical wooden block.
$\therefore $Radius of hemisphere\[\left( r \right) = \dfrac{{{\text{diameter}}}}{2} = \dfrac{l}{2}\]unit.
Therefore surface area of remaining solid
$ \Rightarrow $Surface area of the cuboidal box who’s each edge is of length $l$ unit$ - $Area of top of the hemispherical part$ + $Curved surface area of the hemispherical part.
$ \Rightarrow $Surface area of the cuboidal box who’s each edge is of length $l$ unit\[ = 6{l^2}\]sq. Unit
$ \Rightarrow $Area of top of the hemispherical part\[ = \pi {r^2}\] sq. Unit
$ \Rightarrow $Curved surface area of the hemispherical part\[ = 2\pi {r^2}\] sq. Unit
Therefore surface area$\left( A \right)$ of the remaining solid\[ = 6{l^2} - \pi {r^2} + 2\pi {r^2}\]
\[ = 6{l^2} - \pi {\left( {\dfrac{l}{2}} \right)^2} + 2\pi {\left( {\dfrac{l}{2}} \right)^2} = 6{l^2} - \pi \left( {\dfrac{{{l^2}}}{4}} \right) + \pi \left( {\dfrac{{{l^2}}}{2}} \right)\]
\[A = 6{l^2} + \pi \left( {\dfrac{{{l^2}}}{4}} \right) = \dfrac{{{l^2}}}{4}\left( {\pi + 24} \right)\] Sq. Unit
So, this is the required surface area of the remaining solid.

Note- In such types of questions after cutting the required portion according to the question then the remaining portion we found is not in a standard shape so we cannot determine surface area of the remaining solid directly, so we use the concept which is written above to determine the surface area of the remaining solid, then simplify we will get the required answer.