Question

A heavy brass sphere is hung from a spiral spring and it executes vertical vibration with a period T. The ball is now immersed in non viscous liquid with a density one-tenth that of brass. When set into vertical vibration with the sphere remaining inside the liquid all the time, the period will be
 $\text{A}\text{. }\left[ \dfrac{9}{10} \right]T$
$\text{B}\text{. }T\sqrt{\dfrac{10}{9}}$
 $\text{C}\text{. } \text{Unchanged}$
$\text{D}\text{. }T\sqrt{\dfrac{9}{10}}$

Answer 1

Hint: The vibrations produced in the sphere is a motion called a simple harmonic motion. The time period of a body under simple harmonic motion is given as $T=2\pi \sqrt{\dfrac{k}{m}}$, where k is the spring constant and m is the mass of the body. Check what happens to the values of k and m when the system is immersed in a liquid.
Formula used:
$T=2\pi \sqrt{\dfrac{k}{m}}$

Complete step-by-step solution:
Suppose a body is attached to a spring hanging from a ceiling. This is called a spring body system. If we cause a small disturbance in the body, due to the spring force the body will undergo continuous vibrations. This motion of vibrations of the body is called a simple harmonic motion.

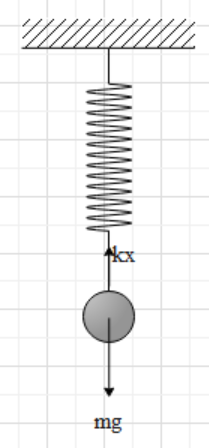
A simple harmonic motion is a period motion. Hence, it has a time period of motion. The time period is defined as the time taken by the body to complete one complete cycle. In a simple harmonic motion, the time period is the time taken by the body to complete one oscillation (to and fro motion).
The time period of the body depends on the spring constant of the spring and the mass of the body.
Suppose the spring constant of the spring is k and the mass of the body is m.
Then the time period of the body is given as $T=2\pi \sqrt{\dfrac{k}{m}}$.
Therefore, the time period of the spring depends on the spring constant and the mass of the body only.

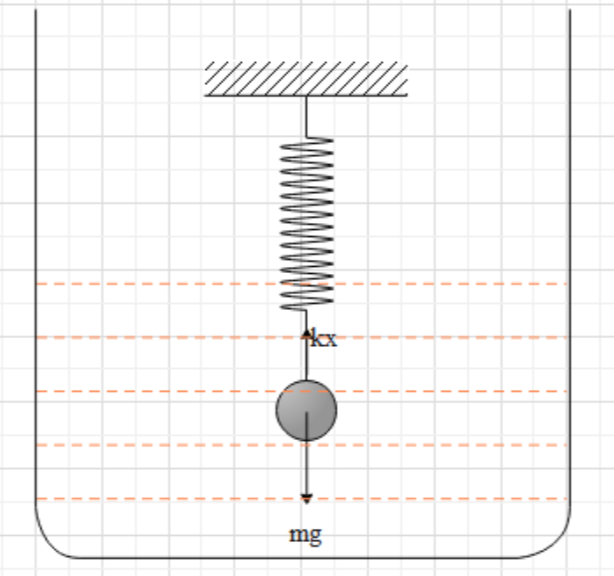
When the system is immersed into a liquid. Neither the spring constant nor the mass of the body changes. Both of the quantities remain the same as they were before immersing in the liquid.
Hence, the time period of the body will remain unchanged.
Therefore, the correct option is C.

Note: Suppose we remove the spring and attach the sphere an inextensible string and produce horizontal vibrations in the sphere. Then the time period of the sphere is given as $T=2\pi \sqrt{\dfrac{l}{{{g}_{eff}}}}$.
Here, l is the length of the string, and ${{g}_{eff}}$ is the effective gravitational acceleration.
In air, ${{g}_{eff}}$=g. Therefore, $T=2\pi \sqrt{\dfrac{l}{g}}$
When we immerse the system in a liquid, due the buoyant force exerted by the liquid on the sphere, the value of ${{g}_{eff}}$ is less than g.
Hence, the time period is more in a liquid than that of in the air.