Question

A guy wire attached to a vertical pole of height \[18m\] is \[24m\] long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Answer 1

Hint: The given pole will be perpendicular (vertical) to ground so we will get a right angle triangle formed by the wire and the vertical pole and the horizontal.
We have the length of the wire and the height of the pole so we can apply Pythagoras theorem to get the value of the base which is the required solution.

Complete step-by-step answer:
It is given that a guy wire attached to a vertical pole of height \[18m\] is \[24m\] long and has a stake attached to the other end.

Here, the height of the vertical pole is \[18m\].
That is \[AB = 18m\]
The wire is \[24m\] long that is \[AC = 24m\].
We need to find out the distance from the base of the pole to another end of the wire which is \[BC\].
Since the pole will be perpendicular (vertical) to ground then,
\[\angle ABC = 90^\circ \] .
Thus we get, \[\Delta ABC\] is a right angle triangle.
Thus we can apply Pythagoras theorem in the right angled $\Delta ABC$,
We get,
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
Substituting \[AB = 18m\] and \[AC = 24m\] we get,
\[ \Rightarrow {(24)^2} = {(18)^2} + B{C^2}\]
Taking squaring for the terms,
\[ \Rightarrow 576 = 324 + B{C^2}\]
Solve it for \[BC\] we get,
\[ \Rightarrow B{C^2} = 576 - 324\]
Subtracting the terms and taking square root on both sides,
\[ \Rightarrow BC = \sqrt {252} \]
Simplifying the root,
\[ \Rightarrow BC = \sqrt {6 \times 6 \times 7} \]
\[ \Rightarrow BC = 6\sqrt 7 m\]

Hence, the stake should be driven \[6\sqrt 7 m\] from the base of the pole so that the wire will be taut.

Note: Pythagoras theorem states that,

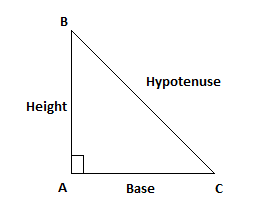
If ABC is a right angled triangle then,
\[{{\text{(Hypotenuse)}}^{\text{2}}}{\text{ = (Height}}{{\text{)}}^{\text{2}}}{\text{ + (Base}}{{\text{)}}^{\text{2}}}\]
\[A{C^2} = A{B^2} + B{C^2}\]