Question

A glass plate of length $10\;cm$, breadth $1.54\;cm$ and thickness $0.20\;cm$ have weight $8.2\;g$ in air. It is held vertically with the long side horizontal and the lower half underwater. Find the apparent weight of the plate. Surface tension of water = $7.3 \times {10^{ - 2}}\;N{m^{ - 1}}$ and $g = 9.8\;m{s^{ - 2}}$.

Answer 1

Hint: A glass plate of a given dimension is immersed with the lower half under the water. Due to the gravity the plate pulls downward and the surface tension repels the force of gravity on the plate. Thus, by finding the resultant of these two forces, the upthrust on the plate is calculated. With help of Newton’s second law, the weight of the plate in water is calculated. The apparent weight of the plate is calculated by finding the difference between the weight of plate in air and weight of plate in water.

Useful formula:
Newton’s second law of motion,
$F = ma$
Where, $F$ is force acted on the body, $m$ is the mass of the body and $a$ is the acceleration of the body.

Relation between mass and volume,
$m = \rho \times V$
Where, $m$ is the mass of the body, $\rho $ is the density of the body and $V$ is the volume of the body.

Relation between surface tension and force,
$T = \dfrac{{{F_t}}}{l}$
Where, $T$ is the surface tension of the water, ${F_t}$ is the force of the body on water and $l$ is the length of body contact with water.

Given data:
Length of the plate, $L = 10\;cm = 10 \times {10^{ - 2}}\;m$
Breadth of the plate, $B = 1.54\;cm = 1.54 \times {10^{ - 2}}\;m$
Thickness of the plate, $t = 0.20\;cm = 0.20 \times {10^{ - 2}}\;m$
Surface tension of water, $T = 7.3 \times {10^{ - 2}}\;N{m^{ - 1}}$
Acceleration due to gravity, $g = 9.8\;m{s^{ - 2}}$
Density of water, $\rho = 1000\;kg{m^{ - 3}}$
Weight of the plate in air, ${w_{air}} = 8.2\;g$

Step by step solution:

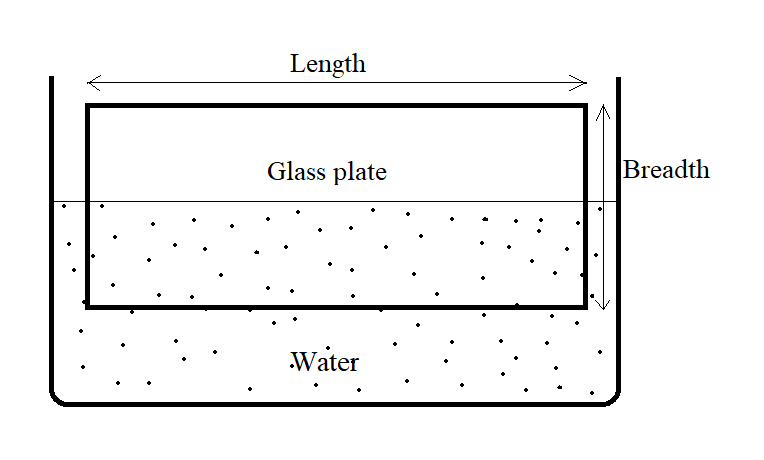
The total volume of the plate which is immersed in water,
$V = L \times t \times \dfrac{1}{2}B$
Substitute the given values, we get
$
  V = 10 \times {10^{ - 2}} \times 0.20 \times {10^{ - 2}} \times \dfrac{1}{2} \times 1.54 \times {10^{ - 2}} \\
  V = 1.54 \times {10^{ - 6}}\;{m^3} \\
 $

By Newton’s second law of motion,
$F = mg$
Substitute the value of $m = \rho \times V$, we get
$F = \rho \times V \times g$
Substitute the given values in above equation,
$
  F = 1000\;kg{m^{ - 3}} \times 1.54 \times {10^{ - 6}}\;{m^3} \times 9.8\;m{s^{ - 1}} \\
  F = 15092 \times {10^{ - 6}}\;N \\
  F = 0.015092\;N \\
 $

Length of the plate immersed in the water is
${l_m} = 2\left( {L + t} \right)$
Substitute the given values in above equation, we get
$
  {l_m} = 2\left( {\left( {10 \times {{10}^{ - 2}}\;m} \right) + \left( {0.20 \times {{10}^{ - 2}}\;m} \right)} \right) \\
  {l_m} = 2 \times {10^{ - 2}}\left( {10 + 0.2} \right) \\
  {l_m} = 2 \times 10.2 \times {10^{ - 2}}\;m \\
  {l_m} = 20.4 \times {10^{ - 2}}\;m \\
  {l_m} = 0.204\;m \\
 $

Downward force on the plate due to surface tension,
${F_d} = {l_m} \times T$
Substitute the given values in above equation, we get
$
  {F_d} = 0.204\;m \times 7.3 \times {10^{ - 2}}\;N{m^{ - 1}} \\
  {F_d} = 1.4892 \times {10^{ - 2}}\;N \\
  {F_d} = 0.014892\;N \\
 $

Hence, the resultant upthrust on the plate is,
${F_{ut}} = F - {F_d}$
Substitute the derived values in above equation, we get
$
  {F_{ut}} = 0.015092\;N - 0.014892\;N \\
  {F_{ut}} = 0.0002\;N \\
 $

Then, the weight of plate immersed in water,
${w_i} = \dfrac{{{F_{ut}}}}{g}$
Substitute the derived values in above equation, we get
$
  {w_i} = \dfrac{{0.0002\;N}}{{9.8\;m{s^{ - 2}}}} \\
  {w_i} = 2.04 \times {10^{ - 5}}\;kg \\
  {w_i} = 2.04 \times {10^{ - 5}} \times {10^3}\;g \\
  {w_i} = 2.04 \times {10^{ - 2}}\;g \\
  {w_i} = 0.0204\;g \\
 $

The apparent weight of the plate will be
${w_a} = {w_{air}} - {w_i}$
Substitute the derived values in above equation, we get
\[
  {w_a} = 8.2\;g - 0.0204\;g \\
  {w_a} = 8.1796\;g \\
 \]

Hence, the apparent weight of the plate is \[{w_a} = 8.1796\;g\]

Note: When the plate is immersed in the water, due to the surface tension the upward thrust will act on the plate. The resultant upthrust is equal to the force of the plate immersed in the water. Hence, the plate applies force on the water due to the acceleration due to gravity. The mass of the plate in water is calculated by using Newton’ law.