Question

A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?

Answer 1

Hint :Assume north to be $ i $ direction and vertically downwards to $ - j $ . Let the rain velocity $ {v_r} $ be $ ai + bj $ . The velocity of the rain observed by the girl is always $ {v_r} - {v_g} $ . Draw vector diagrams for the information given and find $ a $ and $ b $ . We may draw all vectors in the reference frame of the ground-based observer.

Complete Step By Step Answer:
We will separately calculate for both the given cases.
Case-1:
It is given that the velocity of the girl $ {v_g} = 5m/s $ .
We can calculate the velocity of the rain with respect to the girl $ {v_{rg}} $ by using the formula.
 $ {v_{rg}} = {v_r} - {v_g} $

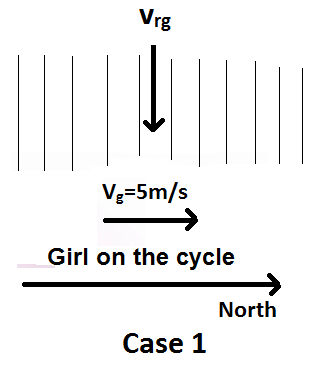
Let the rain velocity $ {v_r} $ be $ ai + bj $ .
 $ \Rightarrow {v_{rg}} = ai + bj - 5i = \left( {a - 5} \right)i + bj $
But, it is given that rain is falling vertically down and therefore, its horizontal component will be zero.
 $
   \Rightarrow a - 5 = 0 \\
   \Rightarrow a = 5 \\
  $
Case-2:
Now, the girl increases her speed to 10 m/s and the rain appears to meet her at 45° to the vertical as shown in the diagram.

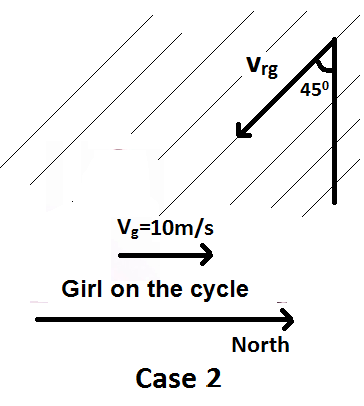
In this case, the velocity of rain with respect to girl is given by:
 $ {v_{rg}} = {v_r} - {v_g} = ai + bj - 10i = \left( {a - 10} \right)i + bj $
As the rain appears to meet the girl at 45° to the vertical as shown in the diagram, we can say that
 $ \tan {45^ \circ } = \dfrac{b}{{a - 10}} $
We know that $ \tan {45^ \circ } = 1 $ and $ a = 5 $ as determined in the first case.
 $
  \dfrac{b}{{5 - 10}} = 1 \\
   \Rightarrow b = - 5 \\
  $
Now we have both the values of $ a $ and $ b $ .
Therefore the velocity of rain $ ai + bj $ is:
 $ {v_r} = 5i - 5j $
And the speed of rain will be:
 $ \left| {{v_r}} \right| = \sqrt {{{\left( 5 \right)}^2} + {{\left( { - 5} \right)}^2}} = \sqrt {50} = 5\sqrt 2 m/s $

Note :
In this question, we have used the concept of relative velocity. Let us consider two objects M and N moving with velocities $ {v_M} $ and $ {v_N} $ respectively with respect to a common stationary frame of reference.
Then, the relative velocity of object M with respect to object N is given as $ {v_{MN}} = {v_M} - {v_N} $ .