Question

A gang capacitor is formed by interlocking a number of plates as shown in figure. This distance between the consecutive plates is 0.885 cm and the overlapping area of the plates is $5\;cm^2$. The capacity of the unit is:

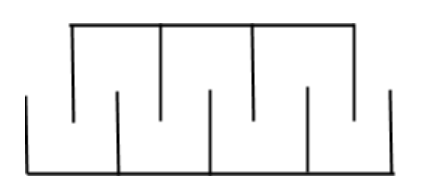
A. 1.06 pF
B. 4 pF
C. 6.36 pF
D. 12.72 pF

Answer 1

Hint: Notice that consecutive plates form a parallel plate capacitor, and consecutive capacitors are arranged in parallel. To this end, determine the capacitance of a single parallel plate capacitor from the values given to us, and consequently determine the net capacitance of the arrangement as an additive sum of individual capacitance.

Formula used: Capacitance $C = \dfrac{A\epsilon_0}{d}$
Net capacitance in parallel $C_{net}= C_1+C_2+….$

Complete step by step answer:
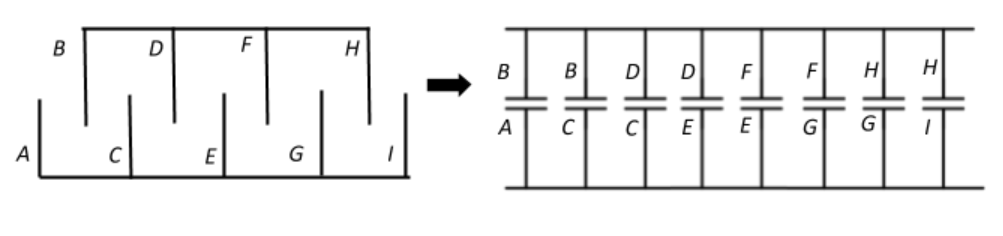
The given arrangement of nine conducting plates is equivalent to eight parallel plate capacitors arranged in parallel to each other as shown in the diagram.

Now, the capacitance of a parallel plate capacitor of area A separated by a distance d in free space can be given as:
$C = \dfrac{A\epsilon_0}{d}$, where $\epsilon_0 = 8.854 \times 10^{-12}\;Fm^{-1}$
Thus, capacitance is proportional to the area of overlap and inversely proportional to the separation between the two conducting plates. The closer the plates are, the greater the capacitance.
Given that $A= 5\;cm^2 = 5 \times 10^{-4}\;m^2$, and
$d = 0.885\;cm = 0.885 \times 10^{-2} = 8.85 \times 10^{-3}\;m$
For any capacitor in the given arrangement, the capacitance will be:
$C = \dfrac{5 \times 10^{-4} \times 8.85 \times 10^{-12}}{8.85 \times 10^{-3}} = 5 \times 10^{-13} = 0.5 \times 10^{-12} = 0.5\;pF$
Now, the effective capacitance of the parallel arrangement will be the sum of all capacitances:
$C_{effective} = C+C+C+….. n\;times = nC$, where n is the number of capacitors.
Since the arrangement contained n=8 capacitors,
$C_{effective} = 8 \times 0.5 = 4\;pF$

So, the correct answer is “Option B”.

Note: Remember that for capacitors in parallel, the net capacitance is the additive sum of individual capacitances, whereas for capacitors in parallel, the reciprocal of the net capacitance is the sum of the reciprocals of individual capacitances. The largest effective capacitance is obtained by connecting the capacitors in parallel, whereas the smallest effective capacitance is obtained by connecting the capacitors in series.
Do not get this confused with resistors, where for resistors in parallel, the reciprocal of the net resistance is the sum of the reciprocals of individual resistances resulting in the smallest effective resistance, whereas for resistors in series, the net resistance is the additive sum of individual resistances, resulting in the largest effective resistance.