Question

A galvanometer of resistance $100\Omega $ has 50 divisions on its scale and has sensitivity of $20\mu A/division$. It is to be converted to a voltmeter with three ranges, of$~0-2V$, $0-10V$ and $0-20V$. In the circuit shown below what must be the value of ${{R}_{1}}$, ${{R}_{2}}$ and ${{R}_{3}}$?

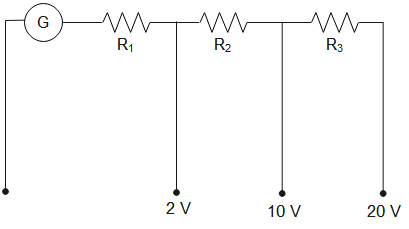
A. ${{R}_{1}}=1900\Omega $
${{R}_{2}}=9000\Omega $
${{R}_{3}}=19900\Omega $
B. ${{R}_{1}}=2000\Omega $
${{R}_{2}}=8000\Omega $
${{R}_{3}}=10000\Omega $
C. ${{R}_{1}}=19900\Omega $
${{R}_{2}}=9900\Omega $
${{R}_{3}}=1900\Omega $
D. ${{R}_{1}}=1900\Omega $
${{R}_{2}}=8000\Omega $
${{R}_{3}}=10000\Omega $

Answer 1

Hint: Determine the maximum current the galvanometer can measure. Then, for each range maximum, determine the expression for current by using Ohm’s law and equate it with maximum current. Solving the equation gives the value of unknown resistance.

Complete step by step answer:
Galvanometer has sensitivity of $20\mu A/division$ and has 50 divisions. Maximum current it can measure is given by
${{I}_{max}}=50\times 20\mu ={{10}^{-3}}A$
When potential of 2 V is applied, the circuit will be as shown below.

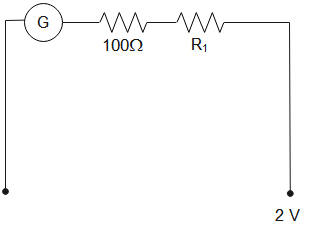
The total resistance through the circuit will be $R={{R}_{G}}+{{R}_{1}}=100+{{R}_{1}}$
Electric current through the circuit will be $I=\dfrac{V}{R}=\dfrac{2}{R}=\dfrac{2}{100+{{R}_{1}}}$
As maximum current the galvanometer can measure is ${{I}_{max}}={{10}^{-3}}A$. Therefore,
$\dfrac{2}{100+{{R}_{1}}}={{10}^{-3}}A$
Solving for ${{R}_{1}}$, we get
${{R}_{1}}=1900\Omega $
When potential of 10 V is applied, the circuit will be as shown below.

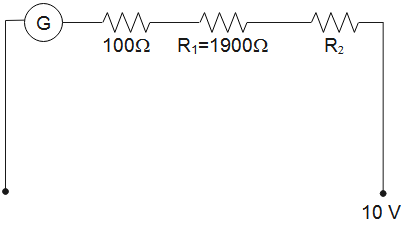
The total resistance through the circuit will be $R={{R}_{G}}+{{R}_{1}}+{{R}_{2}}=100+1900+{{R}_{2}}$
$\Rightarrow R=2000+{{R}_{2}}$
Electric current through the circuit will be $I=\dfrac{V}{R}=\dfrac{10}{R}=\dfrac{10}{2000+{{R}_{2}}}$
As maximum current the galvanometer can measure is ${{I}_{max}}={{10}^{-3}}A$. Therefore,
$\dfrac{10}{2000+{{R}_{2}}}={{10}^{-3}}A$
Solving for ${{R}_{1}}$, we get
${{R}_{2}}=8000\Omega $
When potential of 20 V is applied, the circuit will be as shown below.

The total resistance through the circuit will be $R={{R}_{G}}+{{R}_{1}}+{{R}_{2}}+{{R}_{3}}=100+1900+8000+{{R}_{3}}$
$\Rightarrow R=10000+{{R}_{3}}$
Electric current through the circuit will be $I=\dfrac{V}{R}=\dfrac{20}{R}=\dfrac{20}{10000+{{R}_{3}}}$
As maximum current the galvanometer can measure is ${{I}_{max}}={{10}^{-3}}A$. Therefore,
$\dfrac{20}{10000+{{R}_{3}}}={{10}^{-3}}A$
Solving for ${{R}_{1}}$, we get
${{R}_{3}}=10000\Omega $
Therefore, values of ${{R}_{1}}$, ${{R}_{2}}$ and ${{R}_{3}}$ are $1900\Omega $, $8000\Omega $ and $10000\Omega $ respectively.
Hence, option D is the correct option.

Note:
Ohm’s law gives us the relation between potential and electric current in a circuit. The total resistance in series is equivalent to the sum of the resistance of each resistor connected in series. The sensitivity of the galvanometer is defined as the deflection per unit current flowing through it.