Question

How can a galvanometer be converted into an ammeter?

Answer 1

Hint: A galvanometer is a device that detects current in the circuit. An ammeter is a device that measures the amount of current flowing in the circuit. An ammeter is connected in series. It should measure the current without altering the current. Which means that it must have a very small resistance.

Formula used:
V=iR

Complete step by step answer:
Let us first understand what galvanometer and ammeter are.
A galvanometer is a device that detects a small current in the circuit. It even showed the direction of the current. It is always connected in series in the circuit as shown below.

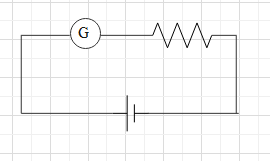
A galvanometer has a small resistance and a small current flow through the galvanometer, the needle deflects to an extent. The direction to which the needle deflects is the direction of the current.
However, a galvanometer only tells us whether there is a current in the circuit. It does not measure the amount of current flowing in the circuit. In addition, a galvanometer has very less tolerance and it can allow a very small current to pass through it. The maximum current that can pass through a galvanometer is ${{i}_{g}}$.
An ammeter is a device that measures the amount of current flowing in the circuit. It is also connected in series to measure the current in a given circuit. An ammeter is made from a galvanometer. Or we can also say that a galvanometer can be converted into an ammeter.
To convert a galvanometer into an ammeter, we connect a resistance R parallel to the galvanometer. This resistance is called shunt resistance. This connection is shown in the figure below.

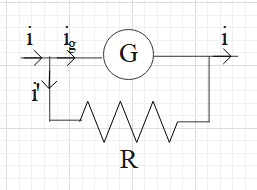
Suppose a current i enters the junction P and it distributes into ${{i}_{g}}$ and i’. The current ${{i}_{g}}$ will flow through the galvanometer and the current i’ will flow through the shunt resistance R.
By applying junction law we get that, $i=i'+{{i}_{g}}$.
$\Rightarrow i'=i-{{i}_{g}}$ …. (i).
The resistance of the galvanometer is already known as is equal to ${{R}_{g}}$.
Since the galvanometer has a resistance ${{R}_{g}}$ and a current ${{i}_{g}}$, the potential difference across its ends is equal to V =${{i}_{g}}{{R}_{g}}$…… (ii). (According to Ohm’s law).
Since the shunt resistance is in parallel connection with the galvanometer, the potential difference across R will be equal to i’R and this will be equal to V.
This implies that V=i’R …. (iii).
Equate (ii) and (iii).
Hence, we get ${{i}_{g}}{{R}_{g}}=i'R$.
Substitute the value of i’ from equation (i).
 $\Rightarrow {{i}_{g}}{{R}_{g}}=\left( i-{{i}_{g}} \right)R$
$\Rightarrow {{i}_{g}}{{R}_{g}}=iR-{{i}_{g}}R$
$\Rightarrow {{i}_{g}}{{R}_{g}}+{{i}_{g}}R=iR$
$\Rightarrow {{i}_{g}}=\dfrac{iR}{\left( {{R}_{g}}+R \right)}$
Since, the galvanometer can accept a very small amount of current, the value R must be very small. When this happens almost all of the current flows through the shunt resistance and the galvanometer is not damaged.
In addition, the net resistance of the ammeter is ${{R}_{net}}=\dfrac{R{{R}_{g}}}{R+{{R}_{g}}}$.
The value of shunt resistance is very small and even the resistance of the galvanometer is also small, the effective resistance of the ammeter will be very less. In fact negligible. And this is the role of an ammeter. The job of the ammeter is measure the current without affecting or disturbing the flow of current in the circuit.

Note:
An ideal ammeter is an ammeter, which measures the current in the circuit without occupying any potential difference. This means that the potential difference across an ideal ammeter is zero and thus does participate in the circuit.
The ammeters that we see in the problems are assumed to be ideal ammeters.