Question

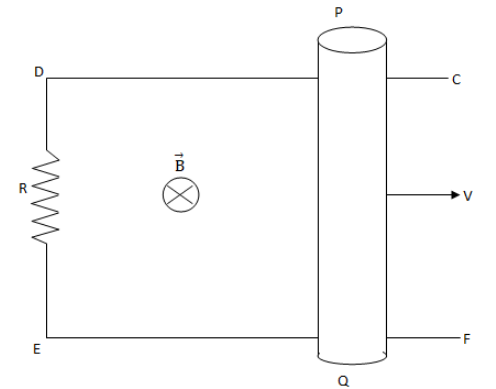
A frame CDEF is placed in a region where a magnetic field \[\overrightarrow B \] is present. A rod of length one metre moves with constant velocity \[20\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}\] and strength of magnitude field is one tesla. The power spent in the process is ( take \[R = 0.2\Omega \] and all other wires and rod have zero resistance).

Answer 1

Hint:We are asked to calculate the power required to move the rod outward with constant velocity \[20\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}\]. For this, you will need to recall the formulas for induced emf, force on the rod due to the magnetic field and power required to move the rod. With the help of these formulas, find the power required.

Complete step by step answer:
Given, a frame CDEF is placed in a region where a magnetic field \[\overrightarrow B \] is present.Length of the movable rod, \[l = 1\,{\text{m}}\].
Velocity of the rod, \[v = 20\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}\].
Strength of magnetic field, \[B = 1\,{\text{Tesla}}\].
Resistance of the rod, \[R = 0.2\Omega \].

As, the rod PQ is moving outward there will be change in magnetic flux through the frame CDEF which will induce an emf in the frame, that is given by the formula,
\[\varepsilon = Blv\]
where \[l\] is the length of the rod, \[B\] is the strength of the magnetic field and \[v\] is the velocity of the rod.
Due to the presence of magnetic field, when the rod PQ moves it will experience a force. This force is given by the formula,
\[F = IlB\] (ii)
where \[I\] is the current through the rod.
To move the rod with constant velocity \[20\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}\], the power needed to given the formula,
\[P = Fv\] (iii)

To find the current, we use the formula
\[I = \dfrac{\varepsilon }{R}\]
Putting the value of \[\varepsilon \] from equation (i) we get,
\[I = \dfrac{{Blv}}{R}\] (iv)
Putting this value of \[I\]in equation (ii) we get,
\[F = \left( {\dfrac{{Blv}}{R}} \right)lB\]
\[ \Rightarrow F = \dfrac{{{B^2}{l^2}v}}{R}\]
Putting this value of \[F\] in equation (iii) we get,
\[P = \left( {\dfrac{{{B^2}{l^2}v}}{R}} \right)v\]
\[ \Rightarrow P = \dfrac{{{B^2}{l^2}{v^2}}}{R}\]
Now, putting the values of \[B\], \[l\], \[v\] and \[R\] we get,
\[ \Rightarrow P = \dfrac{{{1^2} \times {1^2} \times {{20}^2}}}{{0.2}}\]
\[ \Rightarrow P = \dfrac{{400}}{{0.2}}\]
\[ \Rightarrow P = 2000\,{\text{W}}\]
\[ \therefore P = 2\,{\text{kW}}\]

Therefore, the power spent in the process is \[2\,{\text{kW}}\].

Note:According to Faraday’s law of induction, when a closed circuit is placed in the presence of a magnetic field, an electromotive force is induced due to which an induced current is generated in the circuit. And the induced emf is equal to the rate of change of magnetic flux through the circuit.