Question

A flower bed is made in the shape of a sector of a circle. 20 m of wire is available to make a fence for the flower bed. Find the radius of the circle so that area of the flower bed is maximum.

Answer 1

Hint: To solve this question first we should know that if a straight wire is converted into a circle then the length of the wire becomes the circumference of the circle. A sector is a part of a circle between its two radii and the arc next to them that is enclosed. A semi-circle that represents half of a circle is the most common sector of a circle.It is possible to further split a circle containing a sector into two regions known as a Major and a Minor Sector.

Complete step-by-step answer:
Given, a flower bed is made in the shape of a sector of a circle and 20 m of wire is available to make a fence for the flower bed, we need to find the radius of the circle.
Let, the radius of the circle be r and $ \theta $ the angle in radians subtended by the arc at the centre of the circle

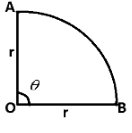
As, the total of the wire is 20 m.
So,
 $ r + r\theta + r = 20 $ , where $ r\theta $ is the arc length.
 $
\Rightarrow 2r + r\theta = 20 \\
\Rightarrow r\theta = 20 - 2r \\
\Rightarrow \theta = \dfrac{{20 - 2r}}{r} \;
  $
As, we know that the area of a sector is given by $ \dfrac{1}{2}{r^2}\theta $ .
So, $ {\text{Area}} = \dfrac{1}{2}{r^2}\theta $ , now substitute the value of $ \theta $ in this equation.
 $
\Rightarrow {\text{Area}} = \dfrac{1}{2}{r^2}\left( {\dfrac{{20 - 2r}}{r}} \right) \\
\Rightarrow {\text{Area}} = \dfrac{1}{2}r\left( {20 - 2r} \right) \\
\Rightarrow {\text{Area}} = \dfrac{{20}}{2}r - \dfrac{{2{r^2}}}{2} \;
\Rightarrow {\text{Area}} = 10r - {r^2} \;
  $
 $ {\text{A}} = 10r - {r^2} $
Now, to maximize the area we need to differentiate it, so differentiate both sides with respect to r.
 $
  \dfrac{{{\text{dA}}}}{{{\text{d}}r}} = \dfrac{{{\text{d}}\left( {10r - {r^2}} \right)}}{{{\text{d}}r}} \\
  \dfrac{{{\text{dA}}}}{{{\text{d}}r}} = 10 - 2r \\
\Rightarrow 10 - 2r = 0 \\
\Rightarrow 2r = 10 \\
\Rightarrow r = \dfrac{{10}}{2} \\
\Rightarrow r = 5\,{\text{m}} \;
  $
So, when the radius of the circle is 5 m, the area of the flower bed is maximum.
So, the area of the flower bed will be $ 10\left( 5 \right) - {5^2} = 50 - 25 = 25\,{{\text{m}}^2} $ .
So, the correct answer is “25 Sq.m”.

Note: The formula for arc length is used to calculate the distance along the curved line that makes up the arc (a part of a circle). The gap that extends along the curved line of the circle making up the arc is defined as the length of the arc, in plain terms. It should be remembered that between its endpoints, the arc length is greater than the straight line width.