
A fish looking up through the water sees the outside world in a circular horizon. If the refractive index of water is $\dfrac{4}{3}$ and the fish is 12cm below the surface, the radius of the circle (in cm ) is :
$A\;.\;36\sqrt 5 $
$B\;.\;4\sqrt 5 $
$C\;.\;36\sqrt 7 $
$D\;.\;\dfrac{{36}}{{\sqrt 7 }}$
Answer
596.4k+ views
Hint: The fish is restricted to see through a circular aperture due to Total Internal reflection. We can find the maximum angle at which a light ray can enter into water and imagine a cone of light rays. The required radius is the radius of the base of this cone, formed at the water-glass interface.
Complete step by step answer:
Let us first see why the fish can only see the world through a circular portion of water.
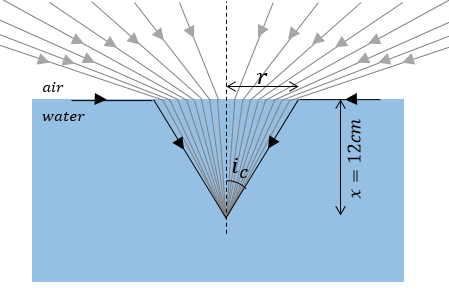
If we imagine light rays coming from the eyes of the fish, then we know that all the rays that hit the water-air interface with an angle lesser than the critical angle would get refracted and reach to the outside world. All the rays with angles greater than the critical angle would be totally internally reflected. Now we know from the principle of reversibility of light that if we reverse the direction of any ray, it would trace back the same path it took. So we can say that all the light coming from the outside world enters the eyes of the fish through a cone. We can see from the diagram that the half-angle of this cone would be the critical angle of the water-air interface.
If we find the critical angle, (which is equal to the half-angle of the cone) then we can easily find the radius of the circle.
We know that a ray coming out of the water at the critical angle would grace the surface of the interface and hence have an angle of refraction of ${90^o}$. Let us say this critical angle of incidence is ${i_c}$. So we can use Snell's law to find the angle of incidence.
$\dfrac{{sin\;{i_c}}}{{sin(90)}} = \dfrac{{{n_a}}}{{{n_w}}} = \dfrac{1}{{4/3}} = \dfrac{3}{4}$.
$sin\;{i_c} = \dfrac{3}{4}$
Now we can see from the diagram that if $r$ is the radius of the circle and $x$ is the depth at which the fish is present, then
$r = x\;tan{i_c}$
Now, since we know $sin{i_c}$, $tan{i_c}$ can be found as :
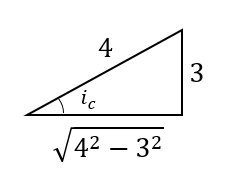
$tan{i_c} = \dfrac{3}{{\sqrt {{4^2} - {3^2}} }} = \dfrac{3}{{\sqrt 7 }}$
So the radius would be: $r = xtan{i_c} = 12cm \times \dfrac{3}{{\sqrt 7 }} = \dfrac{{36}}{{\sqrt 7 }}cm$.
Note: Though the fish sees through a small circle, it is seeing the complete outside world. All light striking the air-water interface with angles ${0^o}$ to ${90^o}$ gets into water with angle of refraction in between ${0^o}$ and ${i_c}$. We can see from the diagram that all rays from the outside are actually coming in. It is just that all of the light gets compressed to fit inside the cone.
Complete step by step answer:
Let us first see why the fish can only see the world through a circular portion of water.

If we imagine light rays coming from the eyes of the fish, then we know that all the rays that hit the water-air interface with an angle lesser than the critical angle would get refracted and reach to the outside world. All the rays with angles greater than the critical angle would be totally internally reflected. Now we know from the principle of reversibility of light that if we reverse the direction of any ray, it would trace back the same path it took. So we can say that all the light coming from the outside world enters the eyes of the fish through a cone. We can see from the diagram that the half-angle of this cone would be the critical angle of the water-air interface.
If we find the critical angle, (which is equal to the half-angle of the cone) then we can easily find the radius of the circle.
We know that a ray coming out of the water at the critical angle would grace the surface of the interface and hence have an angle of refraction of ${90^o}$. Let us say this critical angle of incidence is ${i_c}$. So we can use Snell's law to find the angle of incidence.
$\dfrac{{sin\;{i_c}}}{{sin(90)}} = \dfrac{{{n_a}}}{{{n_w}}} = \dfrac{1}{{4/3}} = \dfrac{3}{4}$.
$sin\;{i_c} = \dfrac{3}{4}$
Now we can see from the diagram that if $r$ is the radius of the circle and $x$ is the depth at which the fish is present, then
$r = x\;tan{i_c}$
Now, since we know $sin{i_c}$, $tan{i_c}$ can be found as :
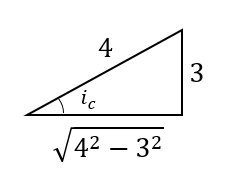
$tan{i_c} = \dfrac{3}{{\sqrt {{4^2} - {3^2}} }} = \dfrac{3}{{\sqrt 7 }}$
So the radius would be: $r = xtan{i_c} = 12cm \times \dfrac{3}{{\sqrt 7 }} = \dfrac{{36}}{{\sqrt 7 }}cm$.
Note: Though the fish sees through a small circle, it is seeing the complete outside world. All light striking the air-water interface with angles ${0^o}$ to ${90^o}$ gets into water with angle of refraction in between ${0^o}$ and ${i_c}$. We can see from the diagram that all rays from the outside are actually coming in. It is just that all of the light gets compressed to fit inside the cone.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




