Question

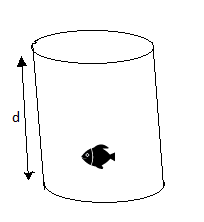
A fish floats in liquid with its eye at the center of an opaque walled full tank of liquid of circular cross-section. When the fish look upwards, it can see a fish-eye view of the surrounding scene i.e. it is able to view the entire space above the liquid surface. The diameter of the tank is 30 cm, and the critical angle for liquid is \[{37^ \circ }\]. At what maximum depth below the surface of the liquid, d must the fish be floating? \[\left( {\sin {{37}^ \circ } = \dfrac{3}{5}} \right)\].

Answer 1

Hint: Here we have to find at what maximum depth below the surface of the liquid the fish must be floating. For that, we consider a triangle and use the trigonometric identities and solve the equation further to get the depth maximum.

Complete step by step answer:
It is given that the diameter of the tank is 30cm which in turn implies that the radius of the tank is 15 cm.
Also given that the critical angle made by fish is \[{37^ \circ }\]and also given that \[\sin {37^ \circ } = \dfrac{3}{5}\]
So using the trigonometric function, we get
\[\Rightarrow \tan {37^ \circ } = \dfrac{3}{4}\]
The fish can see the entire space above the surface, which means the ray coming from its eye must fall at a critical angle at the edge of the liquid surface with this condition we make the following figure.

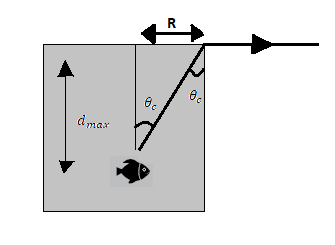
Let us use the relation between angles and sides in the triangle formed we get,
\[\Rightarrow \tan \theta = \dfrac{R}{{{d_{\max }}}}\]
Let us rearrange the equation above as follows,
\[\Rightarrow {d_{\max }} = \dfrac{R}{{\tan \theta }}\]
We know that the radius is 15cm and the angle is \[{37^ \circ }\], we get,
\[\Rightarrow {d_{\max }} = \dfrac{{15}}{{\tan {{37}^ \circ }}}\]
Let us substitute the known values we get,
\[\Rightarrow{d_{\max }} = \dfrac{{15}}{{\dfrac{3}{4}}}\]
By solving the above equation we get the depth maximum as,
\[\Rightarrow {d_{\max }} = 20{\rm{ }}cm\]

Hence, the maximum depth below the surface of the liquid is 20 cm.

Note:
\[\left( {\sin {{37}^ \circ } = \dfrac{3}{5}} \right)\] is given from this we calculate \[\tan {37^ \circ }\]
We know that \[\tan x = \dfrac{{\sin x}}{{\cos x}} = \dfrac{{\sin x}}{{\sqrt {1 - {{\sin }^2}x} }}\]
On substituting the angle we get
\[\tan {37^ \circ } = \dfrac{{\sin 37^\circ }}{{\sqrt {1 - {{\sin }^2}37^\circ } }} = \dfrac{{\dfrac{3}{5}}}{{\sqrt {1 - {{(\dfrac{3}{5})}^2}} }} = \dfrac{3}{4}\]
This is being used in the problem.