Question

A fighter plane flying horizontally at an altitude of \[1.5{\text{ }}km\] with speed \[720{\text{ }}km{h^{ - 1}}\] passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed \[600{\text{ }}m{s^{ - 1}}\] to hit the plane.
(Take \[g{\text{ }} = {\text{ }}10{\text{ }}m{s^{ - 1}}\])
A. \[si{n^{ - 1}}\left( {\frac{1}{3}} \right)\\ \]
B. \[si{n^{ - 1}}\left( {\frac{2}{3}} \right)\\ \]
C. \[co{s^{ - 1}}\left( {\frac{1}{3}} \right)\\ \]
D. \[co{s^{ - 1}}\left( {\frac{2}{3}} \right)\\ \]

Answer 1

Hint:
To solve this question, we will first construct a figure using the given information. Then using a situation, i.e., the horizontal distance travelled by the shell and the distance travelled by the plane must be equal, on putting the values in this situation we will get our required answer.

Complete step by step solution:
We are given that a fighter plane flying horizontally at an altitude of \[1.5{\text{ }}km\] with speed \[720{\text{ }}km{h^{ - 1}}\] passes directly overhead an anti-aircraft gun. We need to find at what angle from the vertical should the gun be fired for the shell with muzzle speed \[600{\text{ }}m{s^{ - 1}}\] to hit the plane.

So, the given height of the fighter plane \[ = {\text{ }}1.5km{\text{ }} = {\text{ }}1500\;m\]
And, the speed of the fighter plane, \[v{\text{ }} = {\text{ }}720km{h^{ - 1}}{\text{ }} = {\text{ }}200\;m{s^{ - 1}}\]
Also, the given muzzle velocity of the gun, \[u{\text{ }} = {\text{ }}600\;m{s^{ - 1}}\;\]

Let $\theta $ be the angle with the vertical so that the shell hits the plane.
Now, let us construct a figure using the above information.

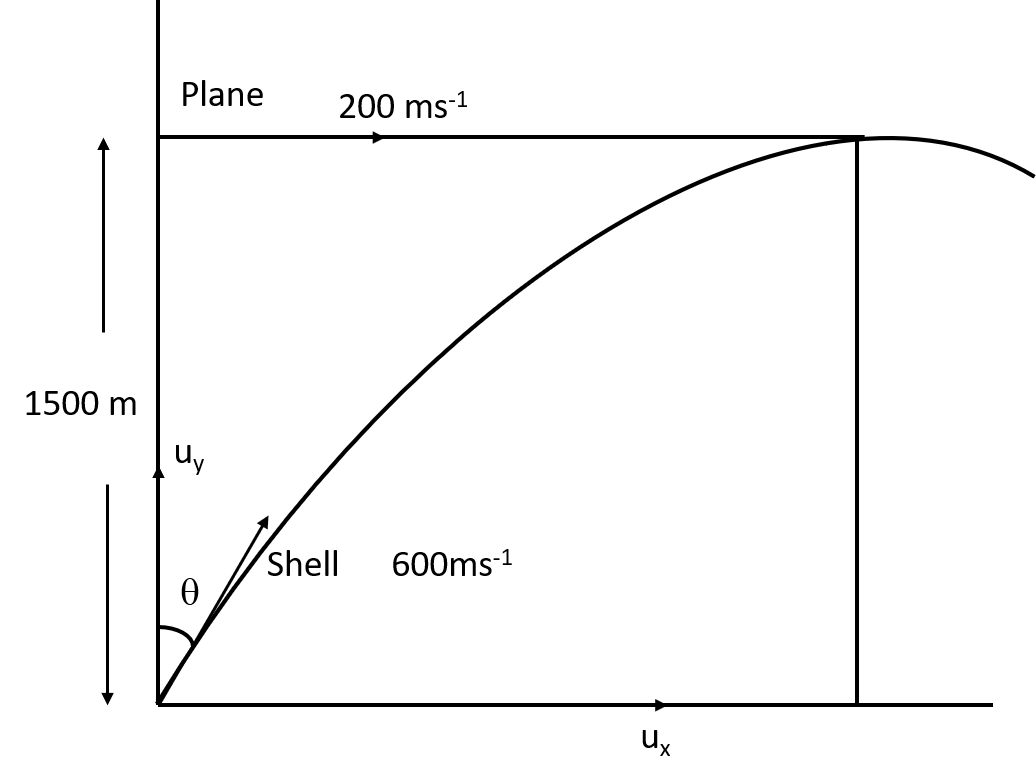
Let the time taken by the shell to hit the plane be t
Then the horizontal distance travelled by the shell \[ = {\text{ }}{u_x}t\]
And the distance travelled by the plane \[ = {\text{ }}vt\]

The shell hits the plane. So, the horizontal distance travelled by the shell and the distance travelled by the plane must be equal.
\[{u_x}t{\text{ }} = {\text{ }}vt\]
Since, it is the horizontal distance, therefore, \[u\;sin\;\theta {\text{ }} = {\text{ }}v\]

\[\sin \theta = \frac{v}{u}\]
On putting the value in the above equation, we get
\[
  {{\text{sin}}\ \ \theta = \frac{{200}}{{600}}{\text{ }} = \frac{1}{3} = {\text{ }}0.33} \\
  \theta = {\text{ }}{\operatorname{Sin} ^{ - 1}}\left( {0.33} \right){\text{ }} \\
  \theta = {\text{ }}{\operatorname{Sin} ^{ - 1}}(\frac{1}{3}) \\
\]
So, the angle from the vertical should the gun be fired for the shell to hit the plane is ${\sin ^{ - 1}}(\frac{1}{3}).$

Thus, option (A) \[si{n^{ - 1}}\left( {\frac{1}{3}} \right),\] is correct.

Note:
In the solutions, students should notice that we have taken the horizontal distance travelled by the shell and the distance travelled by the plane must be equal. Because the distance covered by plane in that time period will be equal to the distance travelled by the shell in a trajectory motion, and it is clearly visible in the figure attached here.