Question

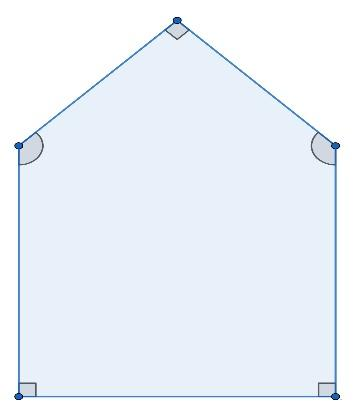
A field is in the shape of a pentagon as shown in the figure. Three of the interior angles of the pentagon are right angles. The remaining two interior angles are congruent. What is the measure of each angle?

Answer 1

Hint: For solving this question firstly we will draw the given figure and consider there is a pentagon ABCDE as per the given configurations. After that, we will take a point O inside the pentagon and join every vertex of it to point O. Then, we will get five triangles and we will use one of the important result that the sum of the interior angles of a triangle is always ${{180}^{0}}$ to find the unknown angles easily.

Given:
It is given that there is a field that is in the shape of a pentagon as shown in the figure. Three of the interior angles of the pentagon are right angles. The remaining two interior angles are congruent, and we have to find the measure of each angle.
Now, let there be a pentagon ABCDE in which $\angle DAB=\angle CBA=\angle DEC={{90}^{0}}$ and $\angle EDA=\angle ECB$ . For more clarity look at the figure given below:

Now, just take a point O inside of the pentagon and join the point O with each vertex of the pentagon as shown in the figure below:

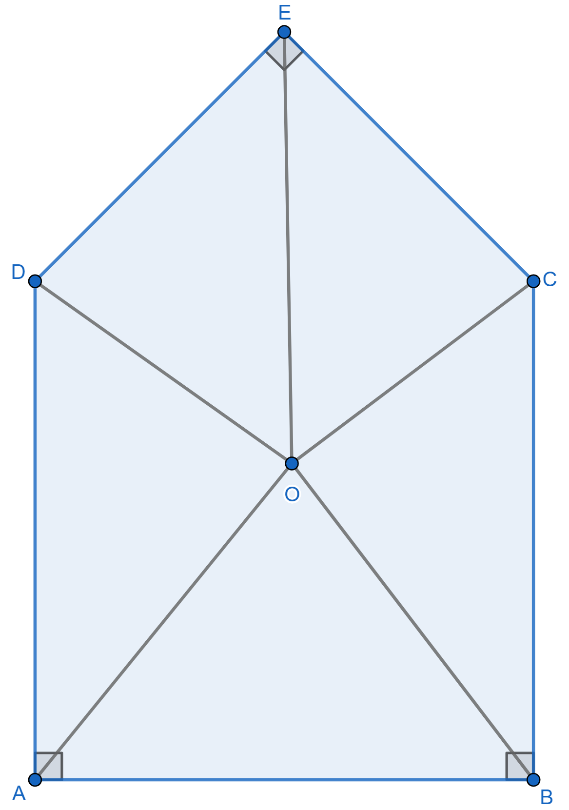
Now, as we know that sum of the interior angles of a triangle is ${{180}^{0}}$ so, sum of the interior angles of the $\Delta AOB,\Delta BOC,\Delta COE,\Delta DOE$ and $\Delta DOA$ will be ${{180}^{0}}\times 5={{900}^{0}}$ . Then,
$\begin{align}
  & \left( \angle AOB+\angle OAB+\angle OBA \right)+\left( \angle BOC+\angle CBO+\angle BCO \right)+\left( \angle COE+\angle OEC+\angle OCE \right) \\
 & +\left( \angle DOE+\angle ODE+\angle OED \right)+\left( \angle AOD+\angle OAD+\angle ODA \right)={{900}^{0}} \\
 & \Rightarrow \left( \angle AOB+\angle BOC+\angle COE+\angle DOE+\angle AOD \right)+\left( \angle OAB+\angle OAD \right)+\left( \angle OBA+\angle CBO \right) \\
 & +\left( \angle BCO+\angle OCE \right)+\left( \angle OED+\angle OEC \right)+\left( \angle ODE+\angle ODA \right)={{900}^{0}} \\
 & \Rightarrow \left( \angle AOB+\angle BOC+\angle COE+\angle DOE+\angle AOD \right)+\angle DAB+\angle CBA+\angle ECB+\angle EDA+\angle DEC={{900}^{0}} \\
\end{align}$
Now, as the lines are concurrent and intersect at point O. So, the value of the $\angle AOB+\angle BOC+\angle COE+\angle DOE+\angle AOD$ will be equal to ${{360}^{0}}$ and it is given that $\angle DAB=\angle CBA=\angle DEC={{90}^{0}}$ and $\angle EDA=\angle ECB$ . Then,
$\begin{align}
  & \left( \angle AOB+\angle BOC+\angle COE+\angle DOE+\angle AOD \right)+\angle DAB+\angle CBA+\angle ECB+\angle EDA+\angle DEC={{900}^{0}} \\
 & \Rightarrow {{360}^{0}}+{{90}^{0}}+{{90}^{0}}+{{90}^{0}}+\angle ECB+\angle ECB={{900}^{0}} \\
 & \Rightarrow {{630}^{0}}+2\angle ECB={{900}^{0}} \\
 & \Rightarrow 2\angle ECB={{270}^{0}} \\
 & \Rightarrow \angle ECB={{135}^{0}} \\
\end{align}$
Now, from the above result, we conclude that the value of $\angle EDA=\angle ECB={{135}^{0}}$ .
Thus, in the given pentagon there will be three angles of ${{90}^{0}}$ and two angles will be of ${{135}^{0}}$ .


Note: Here, we should first understand what is asked in the question and then proceed in the right direction to the correct answer quickly. Moreover, for objective problems, we should use the formula $\left( n-2 \right)\times {{180}^{0}}$ to find the sum of all interior angles of $n$ sided polygon.