Question

A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the farmer at the end of 2 minutes 20 seconds from his initial position?

Answer 1

Hint: Draw the diagram and write the given data. Also find the total time in seconds and total distance travelled in a given time period. Then find displacement.

Complete step by step answer:

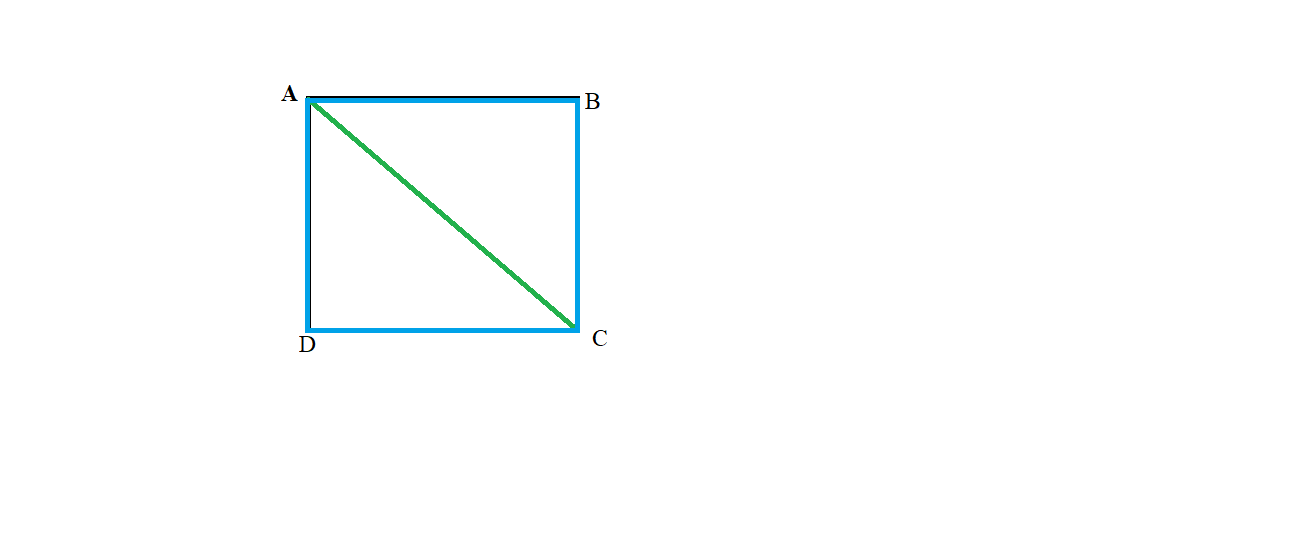
Displacement is the difference between the final position and initial position of a particle or any object. Here first we will draw the diagram.

Perimeter of square = \[4\times a=4\times 10=40m\]
Where a = side of square
Total time taken to travel 40 m is 40 s
So time taken to travel 1 m is $\dfrac{40}{40}=1s$
Since the farmer travels 2 minutes 20 seconds.
2 minutes 20 seconds = $2\times 60+20=140s$
The distance travelled by farmer in 140 s is $140\times 1=140m$
Now, number of rotation to cover 140m along the boundary = total distance perimeter
                                        = $\dfrac{140}{40}=3.5$
That is 3 complete rotations and half rotation
After 3.5 rotations, the farmer will reach at point C
So, the displacement will be AC
AC length can be calculate by using Pythagoras theorem
  \[\begin{align}
  & AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}} \\
 & =\sqrt{{{10}^{2}}+{{10}^{2}}} \\
 & =10\sqrt{2}m \\
\end{align}\]
So after 2 minutes 20 seconds the displacement of the farmer will be equal to $10\sqrt{2}$ m north.

Note: By mistake students can calculate distance instead of displacement. So, Students should remember the difference between distance and displacement. Here distance is 140m but displacement is $10\sqrt{2}$ m north.