Question

A driver of a car approaching a vertical wall notice that the frequency of his car horn has changed from 440 to 480 Hz. When its gets reflected from the wall. Find the speed of the car if the speed of the sound is 300 $m{s^{ - 1}}$.
(A) $16.3m{s^{ - 1}}$
(B) $15.3m{s^{ - 1}}$
(C) $14.3m{s^{ - 1}}$
(D) None of these

Answer 1

Hint :
Above problem is a straightforward formula based problem. Here frequency change is given i.e., initial and final frequency is given and also given the velocity of sound.
So, on putting the values in Doppler effect formula, we get speed of car i.e., $f' = \left( {\dfrac{{v + u}}{{v - u}}} \right)f$
Where
u $ = $ Velocity of car
v $ = $ Velocity of sound
f $ = $ Initial frequency
$f' = $Final frequency

Complete step by step solution :

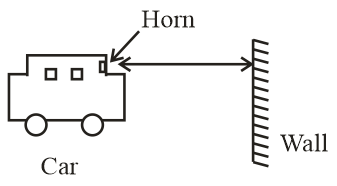
According to Doppler effect, the frequency change is given by
$f' = \left( {\dfrac{{v + u}}{{v - u}}} \right)f$
Given that
f $ = $ 440 Hz
$f' = $ 480 Hz
$v = 300m/s$
$u = ?$
$480 = f' = \left( {\dfrac{{300 + u}}{{300 - u}}} \right)440$
$\left( {\dfrac{{300 + u}}{{300 - u}}} \right) = \dfrac{{480}}{{440}} = \dfrac{{12}}{{11}}$
$11(300 + u) = 12(300 - u)$
$3300 + 11u = 3600 - 12u$
$11u + 12u = 3600 - 3300$
$23u = 300$
$u = \dfrac{{300}}{{23}}$
$u = 13.04m/s$
Hence, the speed of a car is $13.04m/s$.

So, option D is the correct answer.

Note :
1. Observer Light source
     

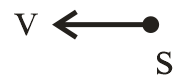
Frequency $f' = \left( {1 + \dfrac{v}{c}} \right)f$
Wavelength $\lambda ' = \left( {1 - \dfrac{v}{c}} \right)\lambda $ Violet shift
2. Observer Light source
     

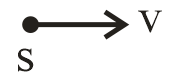
Frequency $f' = \left( {1 - \dfrac{v}{c}} \right)f$
Wavelength $\lambda ' = \left( {1 + \dfrac{v}{c}} \right)\lambda $ Red shift