Question

(a) Draw a schematic sketch of a cyclotron. Explain clearly the role of crossed electric and magnetic fields in accelerating the charge.
Hence, derive the expression for the kinetic energy acquired by the particles.
(b) An $\text{ }\!\!\alpha\!\!\text{ - particle}$ and a photon are released from the centre of the cyclotron and made to accelerate:
(i) Can both be accelerated at the same cyclotron frequency?
      Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit?

Answer 1

Hint: Cyclotron is a device for increasing the velocity of a charged particle by using the fact that an electric field accelerates a charged particle in one direction and the magnetic field rotates the charged particle.

Complete step by step answer:
a) Cyclotron is a device used to accelerate positively charged particles (like $\text{ }\!\!\alpha\!\!\text{ - particle}$, deuterons etc.) to acquire enough energy to carry out nuclear disintegration etc. It is based on the fact that the electric field accelerates a charged particle and the magnetic field keeps it revolving in circular orbits of constant frequency. Thus, a small potential difference would impart enormously large velocities if the particle is made to traverse the potential difference a number of times.

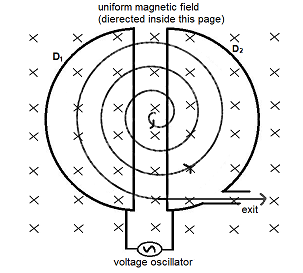
Let us understand how this device works. It consists of two hollow D-shaped metallic chambers D1 and D2 called dees. The two dees are placed horizontally with a small gap separating them. The dees are connected to the source of high frequency oscillating electric fields. The dees are enclosed in a metal box containing a gas at a low pressure of the order of ${{10}^{-3}}mm$ mercury. The whole apparatus is placed between the two poles of a strong electromagnet, which provide the magnetic field. The magnetic field acts perpendicular to the plane of the dees. The positive ions are produced in the gap between the two des by the ionisation of the gas. To produce protons, hydrogen gas is used and to produce alpha particles, helium is used.
Suppose a particle of charge q is released in the gap of the cyclotron. Due to the electric field, a force will act on it i.e ${{F}_{E}}=qE$(E is the magnitude of the electric field). The particle will accelerate and gain some velocity before entering the opposite dees (D1). Now the electric force will not affect the particle due to the absence of an electric field. The magnetic field will exert a force on the particle making it rotate in a circular path. Let us say the radius of that circular path is r and the velocity of the particle is v then the force acting on it will be
${{F}_{B}}=qvB$. Since the particle is rotating it will have a centripetal acceleration i.e. $\dfrac{{{v}^{2}}}{r}$
Therefore, ${{F}_{B}}=qvB=ma=m\dfrac{{{v}^{2}}}{r}$
$\Rightarrow qvB=m\dfrac{{{v}^{2}}}{r}$
$\Rightarrow v=\dfrac{qBr}{m}$
Therefore the kinetic energy of the particle will be $\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}m{{\left( \dfrac{mBr}{m} \right)}^{2}}=\dfrac{{{q}^{2}}{{B}^{2}}{{r}^{2}}}{2m}$.
This way the oscillating electric field accelerates the particle every time when it comes in the middle of the dees and the magnetic field rotates the particle and sends it again into the electric field.

(i) The cyclotron frequency is the frequency of the oscillating electric field. In other words, it is the frequency of the rotation of the charged particles and it is given by $f=\dfrac{Bq}{2\pi m}$. Since photons are not charged particles, f=0 and they will not accelerate. Alpha particles have a charge of 2e, hence their cyclotron frequency will be $f=\dfrac{B(2e)}{2\pi m}=\dfrac{eB}{\pi m}$.

(ii) Since, a photon will not accelerate, the alpha particle will exit the slit with higher velocity, given by ${{v}_{\max }}=\dfrac{qBR}{m}$, where R is the radius of the dees.

Note: The distance between the two dees should be very small so that the frequency of the oscillating electric field and the frequency of the moving particles are the same. The cyclotron cannot accelerate an electron because it has a very small mass and the effect is very less.