Question

A double convex lens of glass $(\mu = 1.5)$ is immersed in water $(\mu = \dfrac{4}{3}).$ If the length in air is F, focal length in water is?
A. $F$
B. $\dfrac{F}{2}$
C. $2F$
D. $4F$

Answer 1

Hint: Let us get some idea about refractive indices. The refractive indices of the lens material and water are not the same. As the refractive index of the medium varies, we may use the lens maker's formula to calculate the focal length of the lens.

Complete answer:
When the subject is in focus, the focal length of the lens is the distance between the lens and the image sensor, normally expressed in millimetres (e.g., 28 mm, 50 mm, or 100 mm). The minimum and maximum focal lengths of zoom lenses are defined, for example, 18–55 mm.
According to the lens maker’s formula,
$ \Rightarrow \dfrac{1}{f} = (\eta - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

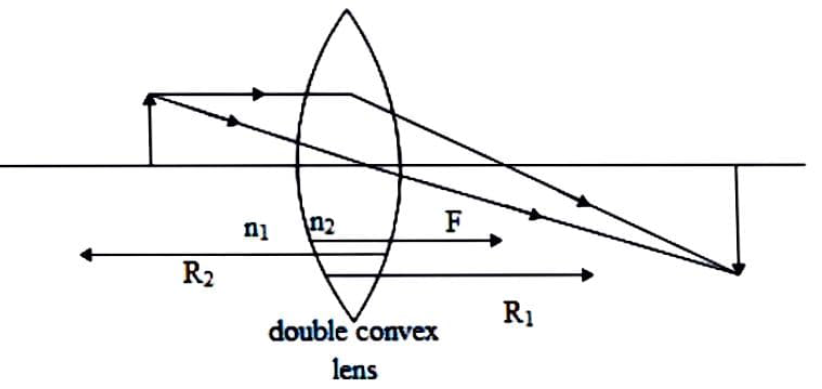
where ${n_1}$ is refractive index of surrounding medium, ${n_2}$ refractive index of lens, \[f\] is the mirror's focal length, $\eta $ is the lens's refractive index in water, \[{R_1}\]is the radius of curvature of the lens surface closest to the light source, and \[{R_2}\]is the radius of curvature of the lens surface furthest from the light source.
$\dfrac{1}{F} = (1.5 - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
$\dfrac{1}{{{F^1}}} = \left( {\dfrac{{\dfrac{3}{2}}}{{\dfrac{4}{3}}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
By dividing above both equation we will get:
$\dfrac{{\dfrac{1}{F}}}{{\dfrac{1}{{{F^1}}}}} = \dfrac{{\dfrac{1}{2}}}{{\dfrac{1}{8}}}$
$ \Rightarrow {F^1} = 4F$
Hence, option D is correct.

Note:
When a lens or glass slab is immersed in a liquid of the same refractive index as the lens, the refractive index of the lens would be equal to \[1\].
The formula used by the lens manufacturer is as follows:
$\dfrac{1}{f} = (1 - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)where,\eta = 1$
$\dfrac{1}{f} = 0$
In this case, the focal length of the lens will tend to infinity.
$f = \infty $.