Question

A cylindrical pipe has an inner diameter of 7 cm and water flows through it at 192.5 liters per minute. Find the rate of flow in kilometers per hour.

Answer 1

Hint:In this question use the direct formula of volume of the cylinder which is $\pi {r^2}h$, here we have to find h as it will give the rate of flow of water. Now the units required is in kilometer per hour so use the concept that 60 minutes makes 1 hour, and 1 liter has $1000{\text{ c}}{{\text{m}}^3}$and 1 km has 100000 cm.

Complete step-by-step answer:

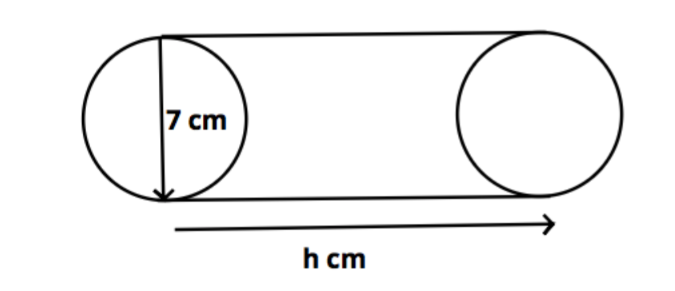
 It is given that volume of water that flows = 192.5 liters/min.
So the volume of water that flows per hour is = $\left( {192.5 \times 60} \right) = 11550$ liters.
(As 1 hour = 60 minutes.)
Now as we know 1 liter = 1000 cm3
Therefore the volume of water that flows per hour is = $\left( {192.5 \times 60 \times 1000} \right)$cm3/hr.
Now the inner diameter of the pipe is 7 cm.
So the radius of the pipe is half of the diameter = $\dfrac{7}{2} = 3.5$ cm.
Now let h be the length of the column of the water that flows in one hour. Clearly the water column forms a cylinder of radius 3.5 cm and length h cm.
Therefore volume of water that flows in one hour = volume of cylinder of radius 3.5 cm and length h cm.
As we know the volume of the cylinder is given as $\left( {\pi {r^2}h} \right)$ cm3.
 $ \Rightarrow \left( {\pi {r^2}h} \right) = \left( {192.5 \times 60 \times 1000} \right)$
$ \Rightarrow h = \dfrac{{\left( {192.5 \times 60 \times 1000} \right)}}{{\dfrac{{22}}{7} \times {{\left( {3.5} \right)}^2}}}$ Cm/hr.
Now as we know 1m = 100 cm
Therefore 1000 m = 1 km = 100000 cm
Therefor $1{\text{ cm = }}\dfrac{1}{{100000}}{\text{ km}}$
$ \Rightarrow \dfrac{{\left( {192.5 \times 60 \times 1000} \right)}}{{\dfrac{{22}}{7} \times {{\left( {3.5} \right)}^2}}}$ Cm/hr = $\dfrac{{\left( {192.5 \times 60 \times 1000} \right)}}{{\dfrac{{22}}{7} \times {{\left( {3.5} \right)}^2}}} \times \dfrac{1}{{100000}}$ km/hr.
Now on simplifying we get,

$ \Rightarrow h = \dfrac{{19.25 \times 6 \times 7}}{{22 \times {{\left( {3.5} \right)}^2}}} = 3$ Km/hr.
So this is the required rate of flow in kilometers per hour.

Note:There must be a question that why have we taken the rate of flow as the height of the cylindrical pipe? The water which flows through the pipe must have been rising only till the height of the pipe and it is constrained inside the pipe walls therefore it’s only the height parameter that can judge the rate flow of water through the pipe.