Question

A cylindrical conductor of radius $R$ is carrying a constant current. The plot of the magnitude of the magnetic field $B$ with the distance $d$ from the center of the conductor, is correctly represented by the figure:
A.

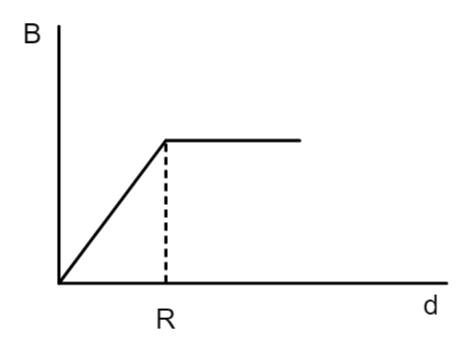
B.

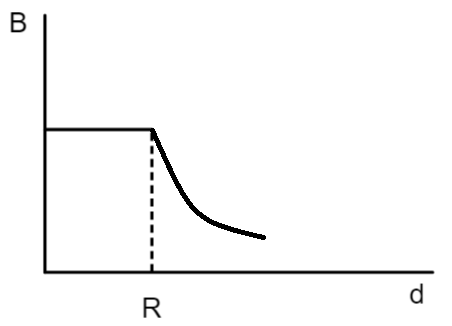
C.

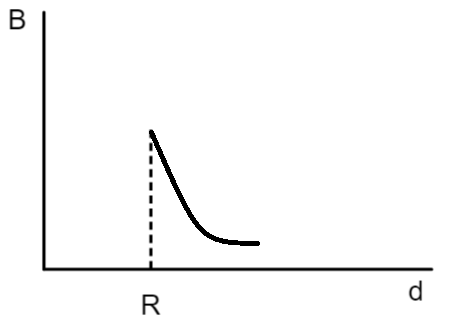
D.

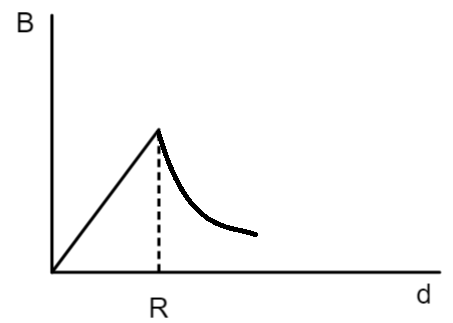
Answer 1

Hint: Use the ampere circuital law to determine the magnitude of magnetic field. Ampere circuital law has to be used for regions inside the cylindrical conductor and the region outside the conductor. Place a graph depicting the relationship between magnetic field and distance from the center.

Formula used:
$\oint{B.dl}={{\mu }_{0}}I$

Complete step by step answer:
Ampere circuital law gives us a mathematical relationship between the current and the magnetic field produced by it. The law states that the line integral of magnetic field intensity along an imaginary closed path is equal to the product of current enclosed by the path and the permeability of the medium. The mathematical form of the law can be written as,
$\oint{B.dl}={{\mu }_{0}}I$
Here, $B$ represents a magnetic field, $dl$ is a small length element, ${{\mu }_{o}}$ is permeability of free space and $I$ is the current which produces magnetic fields.
Now, consider a cylindrical conductor of radius $R$ carrying a constant current $I$. Now, consider an imaginary loop of radius $d$ such that $d${I}'=\dfrac{I}{\pi {{R}^{2}}}\times \pi {{d}^{2}}$
Now, let us find the magnetic field using the ampere circuital law. It can be seen as,
\[\begin{align}
  & \oint{{{B}_{inside}}.dl}={{\mu }_{0}}{I}' \\
 & {{B}_{inside}}\left( 2\pi d \right)={{\mu }_{0}}\left( \dfrac{I}{\pi {{R}^{2}}}\times \pi {{d}^{2}} \right) \\
 & {{B}_{inside}}=\dfrac{{{\mu }_{0}}I}{2\pi {{R}^{2}}}d \\
 & {{B}_{inside}}\propto d
\end{align}\]
Now, let us consider an imaginary loop of radius \[d\] such that $d>R$. Now, the current passing through this loop is equal to $I$. The magnetic field can be calculated as,
\[\begin{align}
  & \oint{{{B}_{outside}}.dl}={{\mu }_{0}}I \\
 & {{B}_{outside}}\left( 2\pi d \right)={{\mu }_{0}}I \\
 & {{B}_{outside}}=\dfrac{{{\mu }_{0}}I}{2\pi d} \\
 & {{B}_{outside}}\propto \dfrac{1}{d}
\end{align}\]
The above obtained relations show that the magnetic field first increases with distance from center linearly till $d=R$ but decreases after it. This type of behaviour can be correctly depicted by the graph below.

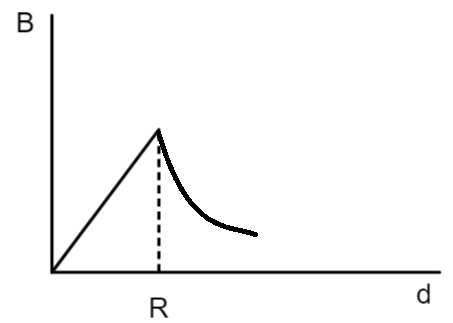
So, the correct answer is “Option D”.

Note:
Correctly determine the amount of current passing through the loop through which magnetic field is to be determined. Correctly interpret the result obtained by the ampere circuital law to obtain a graph. Do not get confused between \[d\] and $R$.