Question

A cylinder containing gas at ${{27}^{{}^\circ }}\,C$ is divided into two parts of equal volumes each $100\,cc$ and at equal pressure by a piston of cross sectional area $10.85\,c{{m}^{2}}$. The gas in one part is raised in temperature to ${{100}^{{}^\circ }}\,C$ while the other is maintained at original temperature. The piston and wall are perfect insulators. How far will the piston move during the change in temperature?
A. $1\,cm$
B. $2\,cm$
C. $0.5\,cm$
D. $1.5\,cm$

Answer 1

Hint: When temperature of an ideal gas is kept constant the product of its pressure and volume is also constant. Due to the difference in pressure on both sides of the cylinder, the piston moves such that pressure on both sides become equal. Use the ideal gas equation to obtain relation between temperature of the gas and length of its container.

Formula used: Ideal gas equation, $PV=nRT$

Complete step by step answer:
According to the ideal gas equation, product of pressure and volume is proportional to its temperature and number of moles.
$PV=nRT$
Initially, the gas on both sides has the same pressure, volume and temperature. This means the quantity of the gas is the same on both sides of the piston.

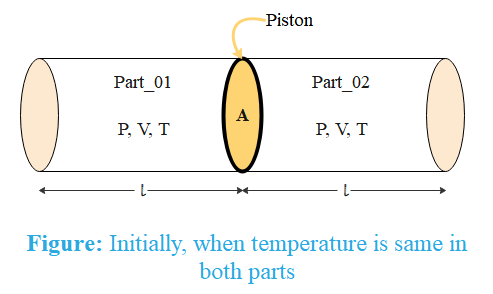
${{n}_{1}}={{n}_{2}}$
Let us denote initial pressure, volume and number of moles on both sides of the piston by $P,\,V\,\text{and }n$ respectively.

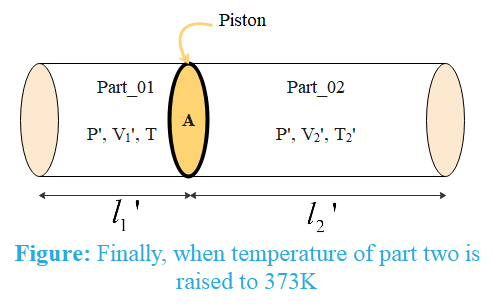
When temperature of part 2 is increased to ${{T}_{2}}'$(say), the ideal gas equation
${{P}_{2}}'{{V}_{2}}'=nR{{T}_{2}}'$
$\Rightarrow {{P}_{2}}'=\dfrac{nR{{T}_{2}}'}{{{V}_{2}}'}$
Where ${{P}_{2}}'\,\text{and}\,{{V}_{2}}'$ are the final pressure and volume of the gas in part 2.
Since piston and walls of the cylinder are insulating, temperature of part 1 do not change, then ideal gas equation for gas in part 1
${{P}_{1}}'{{V}_{1}}'=nRT$
$\Rightarrow {{P}_{1}}'=\dfrac{nRT}{{{V}_{1}}'}$
Since, the piston is in equilibrium, the pressure on both sides of the piston is equal.
${{P}_{1}}'={{P}_{2}}'$
$\Rightarrow \dfrac{nRT}{{{V}_{1}}'}=\dfrac{nR{{T}_{2}}'}{{{V}_{2}}'}$
Volume of the cylinder can be written as $V=Al$ where A is the area of the piston and l is the length of the cylinder. Since area of piston is same for both parts of cylinder, the equation becomes
$\dfrac{nRT}{A{{l}_{1}}'}=\dfrac{nR{{T}_{2}}'}{A{{l}_{2}}'}\Rightarrow \dfrac{{{l}_{2}}'}{{{l}_{1}}'}=\dfrac{{{T}_{2}}'}{T}$
Substituting ${{T}_{2}}'={{100}^{{}^\circ }}C=373K$ and $T={{27}^{{}^\circ }}C=300K$, we get
$\dfrac{{{l}_{2}}'}{{{l}_{1}}'}=\dfrac{373}{300}\Rightarrow {{l}_{2}}'=1.24{{l}_{1}}'$
Assuming, initial length of each part of cylinder to be ${{l}_{1}}\,and\,{{l}_{2}}$ respectively, we get
${{l}_{1}}={{l}_{2}}=l\,(say)=\dfrac{V}{A}=\dfrac{100}{10.85}=9.22cm$
Since total length of cylinder is constant, we have
${{l}_{1}}+{{l}_{2}}={{l}_{1}}'+{{l}_{2}}'$
$\Rightarrow l+l={{l}_{1}}'+1.24{{l}_{1}}'\Rightarrow {{l}_{1}}'=\dfrac{2}{2.24}l=0.89l$
The piston has moved by distance,
${{l}_{1}}-{{l}_{1}}'=l-0.89l=0.11l$
$\Rightarrow {{l}_{1}}-{{l}_{1}}'=0.11\times 9.22=1cm$

So, the correct answer is “Option A”.

Note: Students might use the value of temperature in degree Celsius which is wrong. The temperature value must be in Kelvin.
For a fixed mass of a gas at constant pressure, volume of an ideal gas is directly proportional to absolute temperature of the gas. This is the Charle’s law.