Question

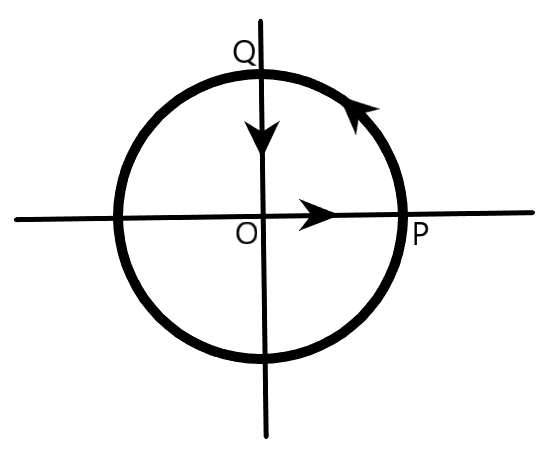
A cyclist starts from the centre $O$ of a circular park of radius $1km$, reaches the edge $P$ of the park, then cycles along the circumference and returns to the centre along $QO$, as shown in the figure. If the round trip takes ten minutes, the net displacement and average speed of the cyclist (in metre and kilometre per hour) are

$\begin{align}
  & A)0,1 \\
 & B)\dfrac{\pi +4}{2},0 \\
 & C)21.4,\dfrac{\pi +4}{2} \\
 & D)0,21.4 \\
\end{align}$

Answer 1

Hint: Displacement of a body is defined as the distance between the final position of the body and the initial position of the body. Average speed of a body is defined as the ratio of total distance of path covered by the body to the total time taken to cover this distance.
Formula used:
$1)$ Displacement = final position – initial position (in $m$)
$2)$ Average speed = (Total distance of path) / (Total time taken) (in $kmh{{r}^{-1}}$)

Complete answer:
We are provided with the information of the motion of a cyclist, in which, the cyclist starts from the centre $O$ of a circular park of radius $1km$, reaches the edge $P$ of the park, then cycles along the circumference and returns to the centre along $QO$, as shown in the following figure. If the round trip takes ten minutes, we are required to calculate the net displacement (in metre) and the average speed of the cyclist (in kilometre per hour).

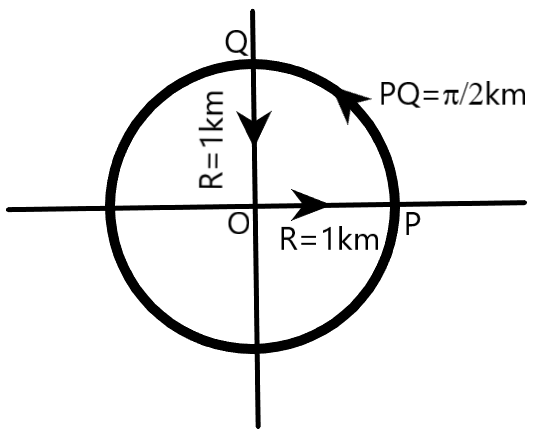
We know that displacement of a body is defined as the distance between the final position of the body and the initial position of the body. Since the initial position and the final position of the cyclist in the given question is the same (point $O$), the net displacement of the cyclist is equal to zero. Mathematically, displacement $(d)$ of the cyclist can be represented as
$d=0m$
Let this be equation 1.
Now, we also know that the average speed of a body is defined as the ratio of total distance of path covered by the body to the total time taken to cover this distance. If ${{S}_{avg}}$ represents the average speed of the cyclist in the given question, then, ${{S}_{avg}}$ is given by
${{S}_{avg}}=\dfrac{(OP+PQ+QO)}{10\min }$
where
$OP+PQ+QO$ is the total distance of the path covered by the cyclist, as clear from the figure.
$10\min $ is the total time taken by the cyclist to cover this distance, as provided in the question.
Let this be equation 2.
Here,
$OP=QO=1km$ because these distances are equal to the radius of the circular path $(R=1km)$, as shown in the figure
Also, it is clear from the figure that
$PQ=\dfrac{2\pi R}{4}=\dfrac{\pi \times (1km)}{2}=\dfrac{\pi }{2}km$
where
$2\pi R=2\pi $ is the circumference of the circular path of radius $R=1km$
Substituting these values in equation 2, we have
${{S}_{avg}}=\dfrac{(OP+PQ+QO)}{10\min }=\dfrac{1km+\dfrac{\pi }{2}km+1km}{10\min }=\dfrac{6(\pi +4)km}{2hr}=3(\pi +4)kmh{{r}^{-1}}=21.42kmh{{r}^{-1}}$
Let this be equation 3.
Therefore, from equation 1 and equation 3, the net displacement and average speed of the cyclist (in metre and kilometre per hour) are $0m$ and $21.42kmh{{r}^{-1}}$, respectively.

So, the correct answer is “Option D”.

Note:
Students need to be thorough with conversion formulas. Conversion formula used in this solution is:
$\begin{align}
  & 1hr=60\min \\
 & 1\min =\dfrac{1}{60}hr \\
 & 10\min =\dfrac{10}{60}hr=\dfrac{1}{6}hr \\
\end{align}$
Also, the value of $\pi $ is taken as
$\pi =3.14$