Question

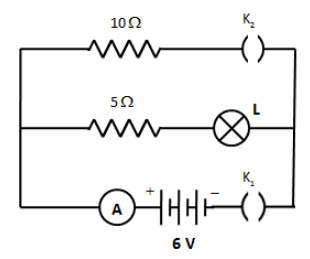
A current of 0.6 A is shown by an ammeter in the circuit when the key \[{{\text{K}}_1}\] is closed. Find the resistance of the lamp L. What change in the current flowing through the resistor and potential difference across the lamp will take place, if the key \[{{\text{K}}_2}\] is also closed. Give reason for your answer.

Answer 1

Hint:Initially, the current will only flow through the arm in which the lamp is connected. Use Kirchhoff’s voltage law to determine the resistance of the lamp. After the key \[{{\text{K}}_2}\] is closed, the current will flow through both the arms. Again, use the KVL to calculate the current in the lamp.

Formula used:
Ohm’s law, \[V = IR\]
where, V is the potential difference, I is the current and R is the resistance.

Complete step by step answer:
Initially, we have given that the key \[{{\text{K}}_2}\] is not closed. Therefore, the current from the battery supply will only flow through the lamp L. We can determine the resistance of the lamp by applying KVL in the first loop containing lamp, \[5\,\Omega \] resistor and battery supply of 6 V. Therefore,
\[ - I\left( {5\,\Omega } \right) - I\left( R \right) + 6\,{\text{V}} = {\text{0}}\]
Here, I is the current flowing through the lamp and \[5\,\Omega \] resistor and R is the resistance of the lamp.

Solving the above equation further, we get,
\[5I + IR = 6\]
\[ \Rightarrow I\left( {5 + R} \right) = 6\]
Substituting 0.6 A for I in the above equation, we get,
\[\left( {0.6} \right)\left( {5 + R} \right) = 6\]
\[ \Rightarrow 5 + R = 10\]
\[ \Rightarrow R = 5\,\Omega \]
Therefore, the resistance of the lamp is \[5\,\Omega \].

Now, when the both the keys are closed, the current at junction A in the circuit will be divided into two parts as shown in the figure below,

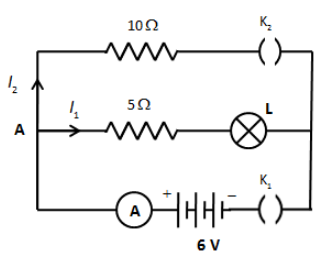
Since the resistance of the lamp is \[5\,\Omega \] and resistance of the resistor just before the lamp is also \[5\,\Omega \], the series resistance of the arm will be \[10\,\Omega \].Applying KVL in the first loop containing lamp, \[5\,\Omega \] resistor and battery supply of 6 V, we get,
\[{I_1}\left( 5 \right) + {I_1}R = 6\,{\text{V}}\]
\[ \therefore {I_1} = 0.6\,{\text{A}}\]
Therefore, the current in the lamp will not change after the key \[{{\text{K}}_2}\] is closed.We know that the potential difference across the parallel combination remains the same. Therefore, the potential across the lamp will remain the same even after the key \[{{\text{K}}_2}\] is closed.We have seen that the current in the lamp has not changed after the key \[{{\text{K}}_2}\] is closed. This is because the resistance of both arms is equal that is \[10\,\Omega \].

Note: To answer these types of questions, students should always use KVL. There are other methods to calculate the current or voltage in the closed circuit but the KVL is most efficient when the circuit involves more than two components. Here, the ammeter shows 0.6 A when the key \[{{\text{K}}_2}\] is open, but the ammeter will show 1.2 A current when the key \[{{\text{K}}_2}\] is closed since the resistance of the circuit decreases.