Question

A current I flows in an infinitely long wire with cross section in the form of a semicircular ring of radius R. The magnitude of the magnetic induction along its axis is
A) $\dfrac{{{\mu _0}I}}{{2{\pi ^2}R}}$
B) $\dfrac{{{\mu _0}I}}{{2\pi R}}$
C) $\dfrac{{{\mu _0}I}}{{4{\pi ^2}R}}$
D) $\dfrac{{{\mu _0}I}}{{{\pi ^2}R}}$

Answer 1

Hint: In this question use the method of integration and take $dl$ as the small length of the infinitely long wire also remember to take the help diagram using the given information, using these instructions will help you to approach towards the solution.

Complete step-by-step answer:
According to the given information we have an infinite wire with a cross section in the form of a semicircular ring with radius R.
Since we know that \[I\] is the current flowing through the wire
Let $d\theta $ be the small angle from the center of the semicircle

So since wire have cross section in shape of semicircle it means
Amount of current flowing through angle $\pi $ is equal to \[I\]
$\pi $ = \[I\]
So in 1 radian current will be = $\dfrac{I}{\pi }$
Therefore current flowing through d$\theta $ will be
$d$\[I\] = $\dfrac{I}{\pi }d\theta $
Now let dB be the magnetic field applied by $d$$\theta $
Since formula of magnetic field is given by $B =$$\dfrac{{{\mu _0}I}}{{2\pi r}}$
Therefore the magnetic field by $d$$\theta $ will be given as
$dB = $$\dfrac{{{\mu _0}dI}}{{2\pi r}}$
Substituting the value of di in the above equation we get
$dB = $\[\dfrac{{{\mu _0}}}{{2\pi r}} \times \dfrac{I}{\pi }d\theta \]
We know that the magnetic field created by the $d\theta $ will be perpendicular to the elementary part of length so let’s find the component of magnetic field which is applying magnetic field along it axis as shown in figure given below

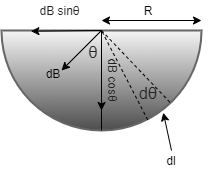
So since as shown in the above diagram that only $dB sin\theta $ is the component that is applying magnetic field along the axis of wire therefore
$dB sin\theta $= magnetic field along the axis of wire = \[\dfrac{{{\mu _0}}}{{2{\pi ^2}r}} \times I\sin \theta d\theta \]
Let $dB sin\theta $ be B magnetic field along axis of wire
Therefore $B =$ \[\dfrac{{{\mu _0}}}{{2{\pi ^2}r}} \times I\sin \theta d\theta \]
Integrating from 0 to $\pi $ in the above equation,
$B =$ \[\int\limits_0^\pi {\dfrac{{{\mu _0}}}{{2{\pi ^2}r}} \times I\sin \theta d\theta } \]
Separating constants from the above equations
$B =$ \[\dfrac{{{\mu _0}I}}{{2{\pi ^2}r}}\int\limits_0^\pi {\sin \theta d\theta } \]
Since we know that $\int {\sin \theta } = - \cos \theta $
Therefore $B = $\[\dfrac{{{\mu _0}I}}{{2{\pi ^2}r}}\left[ { - \cos \theta } \right]_0^\pi \]
$ \Rightarrow $ $B = $\[\dfrac{{{\mu _0}I}}{{2{\pi ^2}r}}\left[ { - \left( {\cos \pi - \cos 0} \right)} \right]\]
Since we know that $\cos \pi = - 1$ and $\cos 0 = 1$therefore we get
$B = $\[\dfrac{{{\mu _0}I}}{{2{\pi ^2}r}}\left[ { - \left( { - 1 - 1} \right)} \right]\]
$ \Rightarrow $ $B = $\[\dfrac{{{\mu _0}I}}{{2{\pi ^2}r}} \times 2\]
$ \Rightarrow $ $B = $\[\dfrac{{{\mu _0}I}}{{{\pi ^2}r}}\]

So the magnetic induction along the axis of wire is \[\dfrac{{{\mu _0}I}}{{{\pi ^2}r}}\].

Hence option D is the correct option.

Note: The concept of magnetic induction that we used in the above solution can be explained as it is an electromagnetic force that is generated across an electric conductor when the magnetic field is changed across the conductor. The magnetic induction occurs until the change in magnetic field across is maintained the more change in rate of magnetic field across the conductor the more magnetic induction occurs.