Question

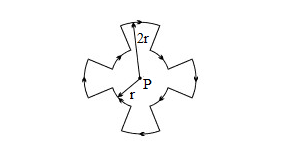
A current I flows around a closed path in the horizontal plane of the circle as shown in the figure. The path consists of eight arcs with alternating radii r and 2r. Each segment of arc subtends equal angle at the common centre P. The magnetic field produced by the current path at point P is

A. \[\dfrac{3}{8}\dfrac{{{\mu _0}I}}{r}\], perpendicular to the plane of paper and directed inward.
B. \[\dfrac{3}{8}\dfrac{{{\mu _0}I}}{r}\], perpendicular to the plane of paper and directed outward.
C. \[\dfrac{1}{8}\dfrac{{{\mu _0}I}}{r}\], perpendicular to the plane of paper and directed inward.
D. \[\dfrac{1}{8}\dfrac{{{\mu _0}I}}{r}\], perpendicular to the plane of paper and directed outward.

Answer 1

Hint: Use the formula for the magnetic field at the centre of circular arc to determine the magnetic field due to both inner and outer arc. The total angle subtended by both the arcs is \[\pi \]. The magnetic field at the centre point P due to straight sections of wire is zero as the current flowing through these sections is perpendicular.

Formula used:
The magnetic field produced by the current carrying arc at the centre of the arc is given as,
\[B = \dfrac{{{\mu _0}I\theta }}{{4\pi r}}\]
Here, \[{\mu _0}\] is the permeability of free space, I is the current, \[\theta \] is the angle subtended by the arc and r is the radius of the arc.

Complete step by step answer:
We know the magnetic field produced by the current carrying arc at the centre of the arc is given as,
\[B = \dfrac{{{\mu _0}I\theta }}{{4\pi r}}\]
Here, \[{\mu _0}\] is the permeability of free space, I is the current, \[\theta \] is the angle subtended by the arc and r is the radius of the arc.
We now calculate the magnetic field at the centre due to current flowing through the outer arc as follows,
\[{B_1} = \dfrac{{{\mu _0}I{\theta _1}}}{{4\pi r}}\]
Here, \[{\theta _1}\] is the angle subtended by the outer arc. We see the angle subtended by the circular coil is \[2\pi \], but in the given question, the angle subtended by the arc is half of the total circular wire. Therefore, the total angle subtended by both the arcs is \[\pi \].
We substitute \[\pi \] for \[{\theta _1}\] in the above equation.
\[{B_1} = \dfrac{{{\mu _0}I\pi }}{{4\pi r}}\]
\[ \Rightarrow {B_1} = \dfrac{{{\mu _0}I}}{{4r}}\]
We now calculate the magnetic field at the centre due to current flowing through the inner arc as follows,
\[{B_2} = \dfrac{{{\mu _0}I{\theta _2}}}{{4\pi \left( {2r} \right)}}\]
Here, \[{\theta _2}\] is the angle subtended by the inner arc.
We substitute \[\pi \] for \[{\theta _2}\] in the above equation.
\[{B_2} = \dfrac{{{\mu _0}I\pi }}{{4\pi \left( {2r} \right)}}\]
\[ \Rightarrow {B_2} = \dfrac{{{\mu _0}I}}{{8r}}\]
The magnetic field at the centre point P due to straight sections of wire is zero as the current flowing through these sections is perpendicular.
Now, the total magnetic field at the centre point P is,
\[B = {B_1} + {B_2}\]
\[ \Rightarrow B = \dfrac{{{\mu _0}I}}{{4r}} + \dfrac{{{\mu _0}I}}{{8r}}\]
\[ \Rightarrow B = \dfrac{{{\mu _0}I}}{r}\left( {\dfrac{1}{4} + \dfrac{1}{8}} \right)\]
\[ \Rightarrow B = \dfrac{3}{8}\dfrac{{{\mu _0}I}}{r}\]
Now we have to determine the direction of the magnetic field at point P using the right hand thumb rule. According to this rule, if we point the thumb of our right hand in the direction of current, then the curl fingers point in the direction of the magnetic field. In this question, we can place a thumb at any place on the wire and the magnetic field will be into the page at any point.

So, the correct answer is option (A).

Note:
You cannot use Fleming’s left hand rule if you don’t know the direction of magnetic force. If you have given only the direction of current, then you can use the right hand thumb rule for the direction of the magnetic field. In the formula for magnetic field at the centre of circular arc, if you put the angle equal to \[2\pi \], then the resultant formula will be the expression for magnetic field at the centre of the current carrying wire loop.