Question

When a current carrying conductor is placed in a magnetic field, a mechanical force is exerted on the conductor which can make the conductor move.

Answer 1

Hint: When a conductor carries current then it generates its own magnetic field around it. When there is an interaction between two magnetic fields there will be attraction and repulsion between them based on the magnetic field direction and the direction of current in the conductor.

Formula used:
Force in magnetic field: $\overrightarrow{F}=I\cdot l\cdot B\sin \theta \hat{n}$

Complete answer:
Suppose a conductor carries current $I$ and it's with the length ($l$). As it is carrying current (DC), some flux lines are going to be generated around the conductor, and that they are concentric with the central axis of the conductor. So, an electromagnetic field is established thanks to this current through this conductor.
Following the right-hand thumb rule, the magnetic flux lines get the direction along with the bent fingers when the thumb denotes the direction of the current flow. The following diagrams represent this rule visually:

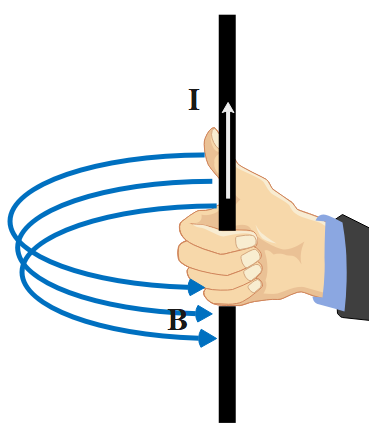
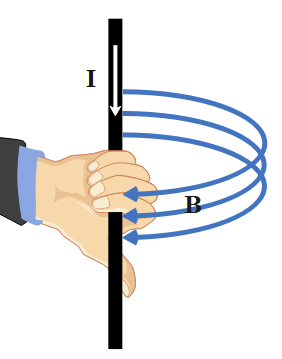
The current carrying conductor is placed between two poles of a horseshoe magnet of flux. This magnet is tightly fixed to the ground. The conductor isn't fixed, rather it's liberal to move. The length of the conductor is simply perpendicular to the permanent magnetic flux of the horseshoe.
So, it's clear that the direction of current and magnetic flux is normal to every other.
The concentric circles of electromagnetic flux thanks to flowing current ($I$) through this conductor attempt to repel the magnetic flux of the static magnet in that situation.
The direction of the present depends on the orientation of the length of the present carrying conductor (I), so the vector is taken for length only. The force $\overrightarrow{F}$ is the cross product of length vector ($\overrightarrow{l}$) and the flux density vector ($\overrightarrow{B}$). Now,
$\overrightarrow{F}=I\cdot l\cdot B\sin \theta \hat{n}$
Here, $\theta $ is the angle between two vectors, and $\hat{n}$ is the unit vector of the force in the perpendicular direction with respect to two vectors direction.
So, this is true that when a current carrying conductor is placed in a magnetic field, a mechanical force is exerted on the conductor which can make the conductor move.

Additional Information:
Fleming’s left rule. By stretching three fingers of the left hand in a perpendicular manner from one another, if the direction of the present is denoted by the finger of the left and therefore the second finger is for the direction of the magnetic flux then the thumb of the left denotes the direction of the conductor’s movement.
Now the direction of the present through this conductor depends on the conductor during which orientation the conductor is placed between two poles of the magnet. Therefore, the current carrying conductor always faces a force within the vicinity of a static magnet or any electro-magnet, supporting this phenomenon of DC motor rotation.

Note:
The force felt by the conductor in the magnetic field depends on the density of the magnetic field so, the greater the magnetic field, the larger the force felt by the conductor and the larger the displacement. But have to take care of the sign convention for the magnetic field.