Question

A cup is in the form of a hemisphere surmounted by a cylinder. The height of the cylindrical portion is 8cm and the total height of the cup is 11.5cm. Find the T.S.A. of the cup.

Answer 1

Hint: In this question, it is given that a hemisphere is surmounted on a cylinder. So, it must look like the following figure.

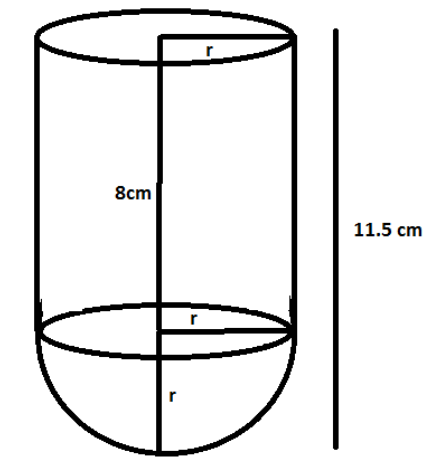
Now, as we know the dimensions of both the cylinder as well as the hemisphere, we can easily calculate the total surface area of the cup by using the following formula.
Total surface area of the cup= CSA of the hemispherical portion of CSA of the cylindrical portion

Complete step-by-step answer:
Now, as we know the dimensions of both the cylinder as well as the hemisphere, we can easily calculate the total surface area of the cup by using the following formula
Total surface area of the cup= CSA of the hemispherical portion of CSA of the cylindrical portion

Now, we must also know that for a hemisphere, the height is equal to the radius and as the hemisphere is surmounted on the cylinder, we can see that the radius of the cylinder and the hemisphere is equal.
As mentioned in the question, we have to calculate the total surface area of the cup.
Now, using the formula given in the hint, we can write as follows

Total surface area of the cup= CSA of the hemispherical portion of CSA of the cylindrical portion
\[\Rightarrow T.S.A.=2\pi {{r}^{2}}+2\pi rh\]
(Because
C.S.A. of a hemisphere \[=2\pi {{r}^{2}}\]
C.S.A. of a cylinder \[=2\pi rh\]
)
Now, we know that the value of r for both cylinder and hemisphere is equal, hence, we can write as follows
\[\Rightarrow T.S.A.=2\pi r\left( r+h \right)\]
Now, we know that the value of h=8 cm and r=11.5-8=3.5 cm (as it is given that the total height that is r+h=11.5cm). So, we can write as follows
\[\begin{align}
  & \Rightarrow T.S.A.=2\pi \times 3.5\times \left( 8+3.5 \right) \\
 & \Rightarrow T.S.A.=2\times \dfrac{22}{7}\times 3.5\times \left( 11.5 \right) \\
 & \Rightarrow T.S.A.=2\times 22\times 0.5\times \left( 11.5 \right) \\
 & \Rightarrow T.S.A.=22\times \left( 11.5 \right) \\
 & \Rightarrow T.S.A.=253\ sq.\ cm \\
\end{align}\]
Hence, the total surface area of the cup is 253 sq. cm.

Note: In this question, it is very important to know that what are the formulae for calculating the curved surface areas of a cylinder and a hemisphere which are given as follows
C.S.A. of a hemisphere \[=2\pi {{r}^{2}}\]
C.S.A. of a cylinder \[=2\pi rh\]
Knowing these formulae becomes very essential as without knowing these, one could never get to the correct answer.