Question

A cube of edge 15 cm is immersed completely in a rectangular vessel containing water. If the dimensions of the base of the vessel are $ 20cm \times 15cm $ , find the rise in water level.

Answer 1

Hint: Let the initial height of the rectangular vessel before immersing the cube be h cm and the rise in level of water after immersing the cube is x cm. So the total height of the water after immersing the cube will be $ \left( {h + x} \right)cm $ . Now the increase in the volume of the water is equal to the volume of the immersed cube.

Complete step-by-step answer:
Volume of a cube is $ {l^3} $ , where l is the length of the edge of the cube.
Volume of a cuboid is $ l \times b \times h $ , where l is the length, b is the breadth and h is the height of the cuboid.

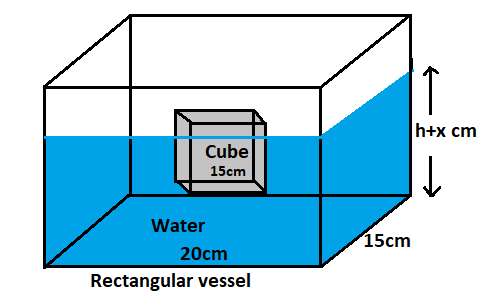
We are given that a cube of edge 15 cm is immersed completely in a rectangular vessel containing water. If the dimensions of the base of the vessel are $ 20cm \times 15cm $ .
We have to find the rise in water level.
The volume of rectangular vessel before immersing is $ l \times b \times h $
 $
\Rightarrow l = 20cm,b = 15cm,h = hcm \\
\Rightarrow Volum{e_{before}} = 20 \times 15 \times h = 300hc{m^3} \\
  $
The volume of rectangular vessel after immersing is $ l \times b \times h $
 $
 l = 20cm,b = 15cm,h = \left( {h + x} \right)cm \\
\Rightarrow Volum{e_{after}} = 20 \times 15 \times \left( {h + x} \right) = 300\left( {h + x} \right)c{m^3} \\
  $
Volume of the cube is $ {l^3} $
 $
\Rightarrow l = 15cm \\
\Rightarrow Volum{e_{cube}} = {15^3} = 15 \times 15 \times 15 = 3375c{m^3} \\
  $
Statement 1: The increase in volume of water is the volume of the rectangular vessel after immersing minus the volume of the rectangular vessel before immersing.
Statement 2: The increase in volume of water is equal to the volume of the cube immersed.
From the above statements we get that,
The volume of the cube immersed is equal to the volume of the rectangular vessel after immersing minus the volume of the rectangular vessel before immersing.
 $
  Volum{e_{cube}} = Volum{e_{after}} - Volum{e_{before}} \\
  Volum{e_{after}} = 300\left( {h + x} \right)c{m^3},Volum{e_{before}} = 300hc{m^3} \\
  Volum{e_{cube}} = 3375c{m^3} \\
 \Rightarrow 3375 = 300\left( {h + x} \right) - 300h \\
 \Rightarrow 300h + 300x - 300h = 3375 \\
 \Rightarrow 300x = 3375 \\
 \Rightarrow x = \dfrac{{3375}}{{300}} \\
  \therefore x = 11.25cm \\
  $
The rise in water level is 11.25cm.

Note: A cube is a three dimensional shape with 6 faces, 8 vertices and 12 edges. A cuboid is also a three dimensional shape which has 6 faces, 8 vertices and 12 edges. But all the edges are equal in a cube but not in a cuboid. The areas and volumes of cube and cuboid are different. So do not confuse a cube with a cuboid.