Question

A copper disc of radius $0.1m$ rotates about its centre with $10$ revolutions per second in a uniform magnetic field of $0.1T$ with its plane perpendicular to the field. The emf induced across the radius of the disc will be given as,
$\begin{align}
  & A.\dfrac{\pi }{10}V \\
 & B.\dfrac{2\pi }{10}V \\
 & C.10\pi mV \\
 & D.20\pi mV \\
\end{align}$

Answer 1

Hint: First of all find the emf across the segment of the disc by taking the product of magnetic field, velocity and the length of the segment. Then find the total induced emf produced across the radius of the disc by taking the half of the product of magnetic field, angular velocity and the square of the radius of the disc. This equation can be obtained by taking the integral of the emf across the segment. These all may help you to solve this question.

Complete answer:
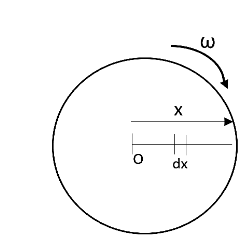
Let us consider a small radial segment of \[dx\] at a distance \[x\] from the centre of the disc. Velocity of this segment is \[\omega x\]. Emf induced across this segment is given as,
\[de=vBL\]
Where \[v\] be the velocity of the disc, \[B\] be the magnetic field and \[L\] be the length. This can be written as,
\[de=vBL=\omega xBdx\]
Now let us find out the emf induced across the radius of \[r\], this can be found by integrating the above mentioned equation. That is,
$\int\limits_{0}^{r}{de}=\int\limits_{0}^{r}{\omega Bxdx}$
Therefore after performing the integration, we can write that,
$\int\limits_{0}^{r}{de}=B\omega \int\limits_{0}^{r}{xdx}$
That is
$E=\dfrac{1}{2}B\omega {{r}^{2}}$
It has been mentioned in the question that,
The frequency is given as,
$\nu =10{{s}^{-1}}$
Therefore the angular velocity will be,
$\omega =2\pi \nu =2\pi \times 10=20\pi rad{{s}^{-1}}$
Magnetic field is given as,
$B=0.1T$
And the radius of the disc is given as,
$r=0.1m$
Substituting all these values in the equation will give,
$\begin{align}
  & E=\dfrac{1}{2}B\omega {{r}^{2}} \\
 & E=\dfrac{1}{2}\times 0.1\times 20\pi \times {{\left( 0.1 \right)}^{2}} \\
 & E=\pi \times {{10}^{-2}}V=10\pi mV \\
\end{align}$

So, the correct answer is “Option C”.

Note:
Angular velocity is given as the measure of how fast a body can rotate or revolves relative to another point. In another way, we can say that how fast the angular position or orientation of an object varies with time. There are two kinds of angular velocity in general. They are orbital angular velocity and spin angular velocity.