Question

A convex mirror has a focal length of 18cm. The image of an object kept in front of the mirror is half the height of the object. What is the distance of the object from the mirror?

Answer 1

Hint: Recall the formation of image by a convex mirror. The image formed by a convex mirror is always a virtual image and cannot be projected on a screen. The image is smaller than the object from the distance but gets larger as the object gets closer to the mirror.
Magnification formula along with mirror formula can be used to obtain the distance of the object from the mirror.

Formula used: Magnification of the object $m=\dfrac{{{h}_{i}}}{{{h}_{o}}}=-\dfrac{v}{u}$
Inverse of focal length $\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$

Complete step by step answer:

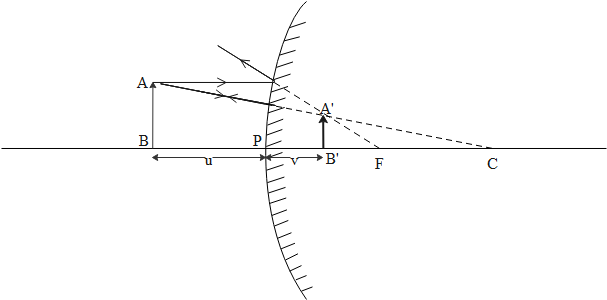
Image formed by the convex mirror is above the principal axis. Therefore the height of the image, ${{h}_{i}}$ will be positive. Due to the same reason, we will also consider the height of the object, ${{h}_{O}}$ as positive. We are provided that the height of the image is half of the object. Mathematically, we can write
$m=\dfrac{{{h}_{i}}}{{{h}_{o}}}=\dfrac{1}{2}$
Where $m=$magnification.
If $v$ is the distance of image from pole of the mirror and $u$ is distance of object from pole then magnification of the object can also be written as
$m=-\dfrac{v}{u}$
We equate this equation with previous equation and get
$-\dfrac{v}{u}=\dfrac{{{h}_{i}}}{{{h}_{o}}}=\dfrac{1}{2}$
$\Rightarrow \dfrac{1}{v}=-\dfrac{2}{u}$
Now we now that, according to mirror formula
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$ where $f$ is the focal length of the mirror.
We are given $f=18cm$. Focal length is taken positively because the convex mirror principal focus lies on the right of the pole of the mirror. We substitute the values and get
$\dfrac{1}{f}=\dfrac{-2}{u}+\dfrac{1}{u}=\dfrac{-1}{u}$
$\Rightarrow u=-f=-18cm$

Thus object is placed at distance 18 cm to the left of the mirror.

Additional Information: Therefore
$v=-\dfrac{u}{2}=-\dfrac{(-18)}{2}$
Or, $v=9cm$.

Note: In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.