Question

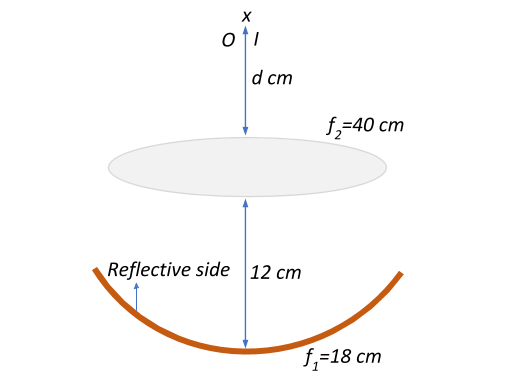
A convex lens of focal length $40\;cm$ is held at a distance $12\;cm$ coaxially above a concave mirror of focal length $18\;cm$. If the convex lens is replaced by a glass plate of thickness $6\;cm$, refractive index $\mu = \dfrac{3}{2}$ and gives rise to an image incident with itself, then the value of d is equal to?

Answer 1

Hint: We are given that the image formed coincides with the object. For a concave mirror this is only possible when the object is placed at the centre of curvature from the pole. In other words, we know that the centre of curvature is at a distance that is twice the focal length. After calculating this, estimate the normal shift of the image and once you have established this, you can equate the “apparent” path length with the object-image coincidence point and calculate d.

Formula Used:
Normal shift $\Delta x = \left[1-\dfrac{1}{\mu}\right]t$, where $\mu$ is the refractive index and t is the thickness of the medium.

Complete step by step answer:
Let us first establish what is given to us.
We have a convex lens that is placed coaxially from a concave mirror that is $12\;cm$ away.
The focal length of the concave mirror is $f_1=18\;cm$
Now, in the place of the convex lens we introduce a glass plate that has a thickness $t = 6\;cm$ and refractive index $\mu = \dfrac{3}{2}$, that is also $12\;cm$ from the concave mirror.
An object ‘O’ is placed at ‘x’. Let us deduce how the light rays from the object behave first when they encounter the concave mirror and then when viewed through the glass slab.

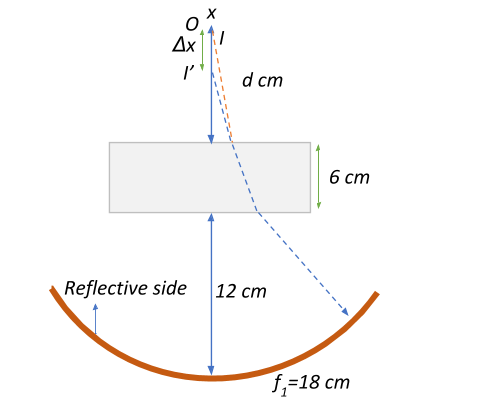
When the light rays pass through the glass slab they undergo refraction and hit the concave mirror at an angle. From what is given, this light gets reflected back from the mirror such that the image ‘I’ also appears to be at ‘x’ for this particular reflective angle.
This is possible only when the object is placed at the centre of curvature of the mirror, i.e., at a distance equal to the radius of curvature ‘R’ from the pole of the mirror. Numerically, the radius of curvature ‘R’ is given as $R = 2f_1 = 2 \times 18 = 36\;cm$.
Therefore, for the mirror, the object and image distances are $u = v = 36\;cm$ respectively.
Now, when you retrace the image path through the glass slab, it appears to be shifted to $I^{\prime}$. This is called the normal shift of the light rays. This is basically an apparent shift in the position of the object that is placed in one medium, and viewed along the normal from another medium. Let us call this shift $\Delta x$.
We can calculate $\Delta x$ using the equation for normal shift that relates it to the thickness ‘t’ of the medium and its refractive index $\mu$:
$\Delta x = \left[1-\dfrac{1}{\mu}\right]t = \left[1-\dfrac{1}{\dfrac{3}{2}}\right] \times 6 = \dfrac{1}{3} \times 6 \Rightarrow \Delta x = 2\;cm$
This means that when viewed normally, the image appears to be at $I^{\prime}$ which is $2\;cm$ before ‘x’.
Now, from above, we know that the image $I^{\prime}$ is “apparently” formed at $36\;cm$. The path that the normal traces to reach $I^{\prime}$ can be given as:
$12+6+d-\Delta x = 36 \Rightarrow 12+6+d-2 = 36 \Rightarrow 16+d = 36 \Rightarrow d= 36 -16 = 20\;cm$.
Thus, we obtain a value of $d= 20\;cm$

Note:
Remember that for a concave mirror the object-image coincidence is possible only when the object is placed at the centre of curvature of the mirror. Also recall that the radius of curvature is twice the focal length.
Do not get confused between lateral shift and normal shift. Lateral shift occurs when there is a “lateral” or sideways shift of the emergent ray, and this ray is parallel to the incident ray. However, normal shift occurs when there is a vertical shift of the emergent ray, and the incident and emergent rays are not necessarily parallel.
Therefore, remember to always account for apparent shifts under the right context.