Question

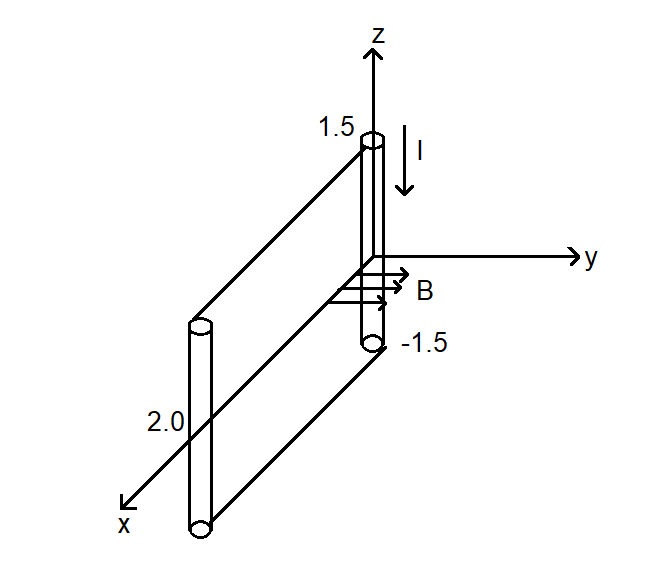
A conductor lies along the z-axis at $ - 1.5m \leqslant x \leqslant 1.5m $ and carries a fixed current of $ 10.0A $ in $ - {\hat a_z} $ direction (see figure). For a field $ \vec B = 3.0 \times {10^{ - 4}}{e^{ - 0.2x}}{\hat a_z}T $ , the power required to move the conductor at constant speed to $ x = 2.0m $ and $ y = 0m $ in $ 5 \times {10^{ - 3}}s $ is (Assume parallel motion along the x-axis)

(A) $ 14.85W $
(B) $ 29.7W $
(C) $ 1.57W $
(D) $ 2.97W $

Answer 1

Hint The power required is given by the work done per unit time. This value will be the work done will be the integration of the force along the x-axis from 0 to 2 meters. So using that value of the work done and the given value of time, we can calculate the power.

Formula Used: In this solution we will be using the following formula,
 $\Rightarrow \vec F = I\vec Bl $
where $ F $ is the force, $ I $ is the current, $ B $ is the magnetic field and $ l $ is the length of the conductor.
 $\Rightarrow W = \int {Fdx} $
Where $ W $ is the work done and $ x $ is displacement
 $\Rightarrow P = \dfrac{W}{t} $ where $ P $ is the power and $ t $ is the time.

Complete step by step answer
 In the problem we are given that a current carrying conductor is placed in a magnetic field then it experiences a force on it. This force is given by the formula, $ \vec F = I\vec Bl $ . In the question we are given $ I = 10.0A $ , $ \vec B = 3.0 \times {10^{ - 4}}{e^{ - 0.2x}}{\hat a_z}T $ and $ l = 1.5 - \left( { - 1.5} \right) $ . So the length is $ l = 3m $ .So substituting the values we get,
 $\Rightarrow \vec F = 10 \times 3 \times 3.0 \times {10^{ - 4}}{e^{ - 0.2x}}{\hat a_z} $
So calculating we get,
 $\Rightarrow \vec F = 9 \times {10^{ - 3}}{e^{ - 0.2x}}{\hat a_z} $
Now the work done is given by the formula, $ W = \int {Fdx} $
Here the limit is from 0 to 2.
So substituting we get,
 $\Rightarrow W = \int\limits_0^2 {9 \times {{10}^{ - 3}}{e^{ - 0.2x}}{{\hat a}_z}dx} $
On integrating we get,
 $\Rightarrow W = \dfrac{{9 \times {{10}^{ - 3}}}}{{\left( { - 0.2} \right)}}\left. {{e^{ - 0.2x}}} \right|_0^2 $
Substituting the values we get,
 $\Rightarrow W = - \dfrac{{9 \times {{10}^{ - 3}}}}{{0.2}}\left( {{e^{ - 0.2 \times 2}} - {e^0}} \right) $
So calculating we get,
 $\Rightarrow W = - 0.045\left( {{e^{ - 0.4}} - 1} \right) $
So we get the work done as,
 $\Rightarrow W = 0.0148J $
Therefore now we can calculate the power as,
 $\Rightarrow P = \dfrac{W}{t} $ . Substituting $ W = 0.0148J $ and $ t = 5 \times {10^{ - 3}}s $ we get,
 $\Rightarrow P = \dfrac{{0.0148}}{{5 \times {{10}^{ - 3}}}}W $
So we get,
 $\Rightarrow P = 2.97W $
Hence the correct answer is option D.

Note
When a current carrying conductor is placed in a magnetic field, then it experiences force acting on it. The direction of the force exerted on the will be given by the right hand rule. If the direction of the magnetic field and the current is perpendicular to each other then the force will be perpendicular to both.