Question

A conductor ab of arbitrary shape carries current \[I\]flowing from b to a. The length vector \[\overrightarrow {ab} \]is oriented from a to b. The force \[\overrightarrow F \] experienced by the conductor in a uniform magnetic field \[\overrightarrow B \] is.
(A) \[\overrightarrow F = - I(\overrightarrow {ab} \times B)\]
(B) \[\overrightarrow F = I(B \times \overrightarrow {ab} )\]
(C) \[\overrightarrow F = - I(\overrightarrow {ba} \times B)\]
(D) All of these

Answer 1

Hint:We should know the formula for force on a current-carrying wire.
We should know the identity of\[(A \times B) = - (B \times A)\].We should know the reversal of a vector \[\overrightarrow {ab} = - \overrightarrow {ba} \].

Complete step by step answer:
A magnetic field is a vector quantity that describes the magnetic influence on moving electric charges, electric currents, and magnetized materials. A charge that is moving in a magnetic field experiences a force normal to its velocity and the magnetic field. Lorentzforce, the force exerted on a charged particle q moving with velocity v through an electric field E and magnetic field B. The entire electromagnetic force F on the charged particle is called the Lorentz force (after the Dutch physicist Hendrik A. Lorentz) and is given by
\[F\; = \;qE\; + \;\left( {qv\; \times \;B} \right)\]
Let us consider a wire of length ab, and a current is passing from b to a.
Then force experienced on the wire is,

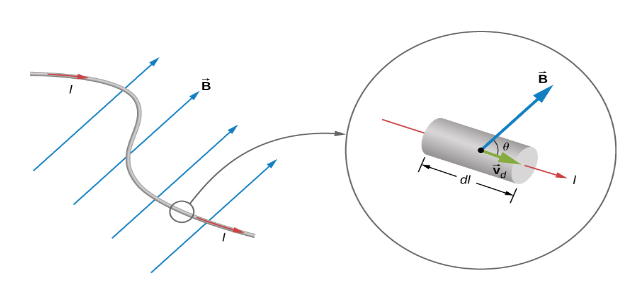
We know that,
\[dF = I(dl \times B)\]
By integrating this we can find the value of F.
\[\int {dF} = \int\limits_b^a {I(dl \times B)} \]
\[\int {dF} = I\int\limits_b^a {(dl \times B)} \]
\[F = I(ba \times B)\]- - - - - - - - - - - - - - - - - - (1)
So Option (C) is correct.
We know that \[\overrightarrow {ab} = - \overrightarrow {ba} \] . - - - - - - - - - - - - - - - - - - (2)
By rearranging (1) using (2)
We get,
\[F = I(ba \times B) = - I(ab \times B)\]- - - - - - - - - - - - - - - - - - (3)
Hence Option (A) is correct.
Again we know that \[(A \times B) = - (B \times A)\]- - - - - - - - - - - - - - - - - - (4)
By rearranging (3) using (4),
we get,
So,
\[\begin{gathered}
F = - I(ab \times B) \\
= - I( - B \times ab) \\
= I(B \times ab) \\
\end{gathered} \]
Since options (A), (B), (C) are correct, hence the correct Option is (D)

Note: You should be aware of vector identities.If any two options are correct, then no need to find the other one since there is an option of all are correct. ( you can save time)
You should also be aware and careful about sign conversion.