Question

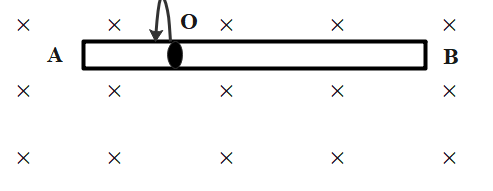
A conducting rod AC of length 4l is rotated about a point O in a uniform magnetic field $\overrightarrow{B}$direction into the paper AO=l and OC=3l. Then

A. ${{V}_{A}}-{{V}_{O}}=\dfrac{B\omega {{l}^{2}}}{2}$
B. ${{V}_{O}}-{{V}_{C}}=\dfrac{7}{2}B\omega {{l}^{2}}$
C. ${{V}_{A}}-{{V}_{C}}=4B\omega {{l}^{2}}$
D. ${{V}_{C}}-{{V}_{O}}=\dfrac{9}{2}B\omega {{l}^{2}}$

Answer 1

Hint: When a conducting rod is placed in a magnetic field B then it experiences a certain force. The rotating rod will contain some amount of emf. Thus, the potential difference between two points can be calculated.

Complete answer:
The potential difference between point O and A is \[{{V}_{O}}-{{V}_{A}}\].
The potential difference between point O and C is \[{{V}_{O}}-{{V}_{C}}\].
Thus, the potential difference between A and C is,
${{V}_{A}}-{{V}_{C}}=({{V}_{O}}-{{V}_{A}})-({{V}_{O}}-{{V}_{C}}).......(i)$
For a rotating rod, the electromotive force (emf) is given as,
$e=\dfrac{BVl}{2}$
Since, the angular velocity $(\omega )$ is
$\omega =V/l$
Rewriting the equations, we get,
$e=\dfrac{B\omega {{l}^{2}}}{2}$
Thus, to calculate total emf for the length, we write,
$de=B\omega l.dl$
For the potential difference between A and O,
$\begin{align}
  & {{V}_{O}}-{{V}_{A}}=\int\limits_{0}^{l}{B\omega l.dl} \\
 & {{V}_{O}}-{{V}_{A}}=\dfrac{B\omega {{l}^{2}}}{2} \\
\end{align}$
For the potential difference between O and C,
$\begin{align}
  & {{V}_{O}}-{{V}_{C}}=\int\limits_{0}^{3l}{B\omega l.dl} \\
 & {{V}_{O}}-{{V}_{C}}=\dfrac{9B\omega {{l}^{2}}}{2} \\
\end{align}$
Thus, the potential difference between the point A and C from equation (i),
\[\begin{align}
  & {{V}_{A}}-{{V}_{C}}=\dfrac{9B\omega {{l}^{2}}}{2}-\dfrac{B\omega {{l}^{2}}}{2} \\
 & {{V}_{A}}-{{V}_{C}}=4B\omega {{l}^{2}} \\
\end{align}\]

Hence, the option C is correct.

Note:
The potential difference depends on the length of the conducting rod. When a conducting rod is placed in a magnetic field then the direction of the flow of electrons and the direction of magnetic field turns to rod producing a torque which results in an electromotive force.