Question

A composite rod of mass 2m and length 2l comprises two identical rods joined end to end at P. The composite rod hinged at one of its end is kept horizontal as shown in the figure. If it is released from rest, find its angular speed when it becomes vertical.

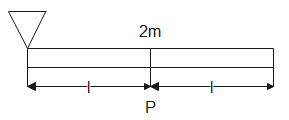
A. $\omega = \sqrt {\dfrac{{3g}}{{2l}}} $

B. $\omega = \sqrt {\dfrac{{5g}}{{2l}}} $

C. $\omega = \sqrt {\dfrac{{7g}}{{2l}}} $

D. $\omega = \sqrt {\dfrac{{9g}}{{2l}}} $

Answer 1

Hint: There is one law which will be valid anywhere and at any situation universally and that law is law of conservation of energy. That means energy can neither be created nor destroyed but it is only converted from one form to the other. By using this law we will solve this problem.

Formula used:
$P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f}$
$U = mgh$

Complete answer:
When we do any work against the conservative force then the work done by us will be stored in the form of potential energy in the system and potential energy increases. Along the direction of conservative force then potential energy of the system decreases.
Here in this problem the rod will be rotating from the horizontal position to vertical position. That means the center of mass of the rod is moving in a downward direction. Potential energy is lost as it is moving along the conservative gravitational force.
If potential energy is lost, as energy can neither be created nor destroyed some other energy must be gained. There are no energies involved here except potential and kinetic energies. Hence the initial potential energy is lost and converted to rotational kinetic energy.
From the below diagram we can see that initially at lower level its has angular velocity $\omega $ so that it has rotational kinetic energy $\dfrac{1}{2}I{\omega ^2}$ there and it is gained from loss of potential energy $2mgh$

If we apply the mechanical energy conservation we will get
$P.{E_i} + K.{E_i} = P.{E_f} + K.{E_f}$
Potential energy is given as $U = 2mgh$
$\eqalign{
 & 2mgl + 0 = 0 + \dfrac{1}{2}I{\omega ^2} \cr
 & \Rightarrow \dfrac{1}{2}I{\omega ^2} = 2mgl \cr
 & \Rightarrow \dfrac{1}{2}\left( {\dfrac{{2m{{\left( {2l} \right)}^2}}}{3}} \right){\omega ^2} = 2mgl \cr
 & \therefore \omega = \sqrt {\dfrac{{3g}}{{2l}}} \cr} $

Hence option A will be the answer.

Note:
When calculating the potential energies we considered half the length of the rod because the center of mass of rod lies there only. We assume the entire mass of the rod is concentrated there and moving down to gain kinetic energy. Hence potential energy lost in that motion will be converted to rotational kinetic energy.